Střídavý proud

            Pod tímto pojmem rozumíme elektrický proud, jehož velikost i směr se s časem mění. Pokud má tato změna periodický charakter, označujeme tento průběh periodický, periodu značíme T.

            Dále určujeme frekvenci, která udává počet kmitů za jednu sekundu. Jednotkou frekvence je herz (Hz = s^-1)

Platí vztah f = 1/T

Příklad: Kmitočet sítě má frekvenci 50 Hz. Určete jeho periodu T = 1/50 s = 20 ms.

Periodické průběhy graficky znázorníme tak, že na osu nanášíme čas t a na osu y okamžité hodnoty proudu nebo napětí.

            Příkladem periodického průběhu je průběh obdélníkový, pilovitý, trojúhelníkovitý, apod. Nejdůležitější ze všech je průběh sinusový, kterým se budeme v této publikaci dále zabývat. Vzniká např. v generátorech v elektrárnách. Příčinou jeho vzniku je otáčivý pohyb vodiče v magnetickém poli (viz elektromagnetická indukce). Kapitoly o magnetismu najde čtenář v [3].

            Platí pravidlo, že každý periodický průběh (např. obdélníkový) vzniká superpozicí (součtem) několika průběhů sinusových.

Funkci y = sin a nebo také i = I_max sin a nebo u = U_max sin a vytvoříme časovým rozvojem kruhového pohybu. Představte si bod, který obíhá po kružnici. Sinusový průběh získáme, znázorníme-li graficky hodnotu jeho ypsilonové souřadnice v závislosti na čase.

            Tato y souřadnice je okamžitá hodnota napětí (proudu), kterou značíme u (i). Poloměr kružnice neboli maximální hodnota napětí (proudu) – amplituda se značí U_max, I_max (nebo také U_m, I_m).

Argument funkce sinus, úhel a se mění v závislosti na čase. Doba jednoho oběhu perioda T odpovídá úhlu 2π rad.

Zavedeme pojem úhlová frekvence w, jejichž jednotkou je radián. Radián je úhel, jehož ramena vytínají na jednotkové kružnici opsané z vrcholu úhlu oblouk délky rovnající se jedné. Úhel 360° = 2π (rad), 180° = π (rad), 90° = π/2 rad.    1 rad. = 360/2π = 57°

Platí w = 2π/T              úhel a odpovídá wt

 

 

 

 

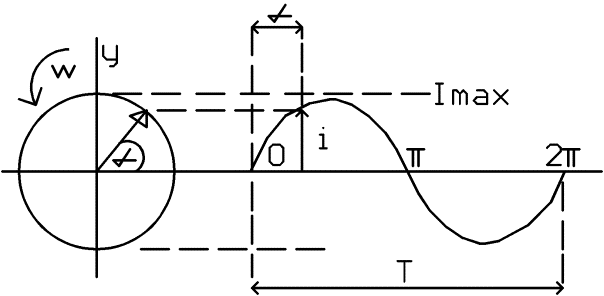
Obrázek: Vznik sinusového průběhu (w = w)

Původní rovnici i = I _max sin a   upravíme na tvar i = I_max wt (u = U_max wt), kde wt je úhel v radiánech.

            V případě, že je počátek sinusového kmitu posunut o úhel j před časovým počátkem, bude mít výše uvedená rovnice tvar i (u) = I_max (U_max) . sin(wt + j), kde j je fázový posuv.

Příklad: Určete okamžitou hodnotu napětí v čase t = 0,02 ms je-li U_max = 5 V a f = 8,33 kHz

T = 0,12 ms      a(t) = 2π f (t) = 6,28 . 8,33 . 10³ . 0,02 . 10^-3 = 1,04 (rad) = 60° 

(Všimněte si, že za jednu šestinu periody se změnil úhel a o 1/6 z 360°)

u = 5 . sin 60° = 5 . Ö 3/2 = 4,33 (V)

Kdy dosáhne okamžitá hodnota napětí svého maxima?

Pro úhel a = 90° = π /2 bude u = U_max. sin 90° = U_max                   

sin 90° = 2πf t              90° = (2π/T) t               π/2 = (2π/T) t

t = T/4              T = 1/f = 0,12 ms                      t = 0,03 ms (v jedné čtvrtině periody)

 

Okamžitá hodnota střídavého proudu nebo napětí není příliš důležitý údaj. Nejvíce nás zajímají celkové účinky střídavého proudu a napětí v porovnání se stejnosměrným proudem a napětím.

Pokud po dobu jedné půlperiody měříme v dostatečně krátkých intervalech okamžité hodnoty proudu (napětí) a vypočítáme z nich aritmetický průměr, dostaneme střední hodnotu střídavého proudu (napětí).

            Střední hodnota střídavého proudu se rovná hodnotě stejnosměrného proudu, který za stejný čas přenese stejný náboj (má stejné elektrochemické účinky, vyloučí z elektrolytu stejné množství kovu.

            Výpočet aritmetického průměru okamžitých hodnot provádíme pomocí integrálů. Ke každému průběhu zadanému matematickou funkcí můžeme vypočítat jeho střední hodnotu. Pro sinusový průběh platí

I_střední = I_max . 2/π = 0,637 I_max                       U_střední = U_max. 2/π

Nejdůležitějším údajem u střídavého proudu a napětí je jeho efektivní hodnota. Jedná se o velikost ekvivalentního stejnosměrného proudu (napětí), který dodává do stejné odporové zátěže stejný tepelný výkon. Z předcházejících kapitol již víme, že výkon je úměrný druhé mocnině proudu a napětí P = U²/R, P = RI²

Dosadíme-li do těchto rovnic vzorec pro okamžitou hodnotu střídavého napětí (proudu), zjistíme, že okamžitá hodnota výkonu je úměrná funkci sin² wt     p = (U_max²/R).sin² wt

            Zprůměrňováním (integrací) okamžitých hodnot výkonu získáme jeho průměrnou hodnotu, ze které vypočítáme efektivní hodnotu napětí (proudu). K získání efektivní hodnoty musíme zprůměrňovat funkci sin² wt a výsledek odmocnit.

            Pro sinusový průběh takto dostaneme velmi důležitý vztah

U_max = Ö 2 U_efektivní = 1,41 U_efektivní                I_m = Ö2 I_ef

U_{ef ektivní} = 0.707 U_max

Efektivní hodnota střídavého proudu a napětí je hodnotou nejdůležitější a základní. Ukazují ji téměř všechny měřící přístroje. Označujeme ji obvykle velkým písmenem bez indexu (U, I). Hovoříme-li o střídavém napětí a proudu, máme automaticky na mysli jeho efektivní hodnotu. (Napětí U = 230 V v síti udává efektivní hodnotu tohoto napětí).

 

            Vznik střídavého napětí v cívce nastává změnou magnetického toku f, který prochází jádrem cívky.                        u = N. dØ/dt, kde N je počet závitů cívky.

Indukované napětí je přímo úměrné změně magnetického toku za jednotku času.

            Bude-li mít tento magnetický tok sinusový průběh Ø = Ø_max sin wt, bude mít sinusový průběh i indukované napětí.

            Největší změna magnetického toku nastává při průchodu nulou, tehdy je největší indukované napětí. Indukované napětí je kladné, pokud magnetický tok roste. Pokud je změna magnetického toku nulová, je i indukované napětí nulové.

            Matematicky se dá dokázat (pomocí derivací, derivace sin x = cos x, derivace cos x = - sin x), že časovou změnou střídavého magnetického toku se v ideální cívce indukuje střídavé napětí, které předbíhá magnetický tok o π/2. Ideální cívka je zhotovena z dokonalého vodiče s nulovým elektrickým odporem, neuplatňují se u ní mezizávitové kapacity.

            Dá se odvodit velikost tohoto indukovaného napětí U = 4,44 f N Ø_max

            Střídavé napětí rovněž vzniká pohybem vodiče v magnetickém poli. Pokud se v homogenním magnetickém poli pohybuje vodič po obvodu kružnice obvodovou rychlostí v = w r, indukuje se v něm podle indukčního zákona napětí okamžité hodnoty u = B l v_x, kde v_x je složka rychlosti kolmá ke směru magnetického pole. Její velikost je

v_x = v sin wt  = w r sin wt

u = B l v_x sin wt = B l w r sin wt, kde B je magnetická indukce pole, l délka vodiče.

Pokud se v homogenním magnetickém poli otáčí jeden závit obdélníkového tvaru, indukují se na obou stranách závitu stejně velké okamžité hodnoty napětí takového smyslu, že se jejich velikosti sčítají.

 

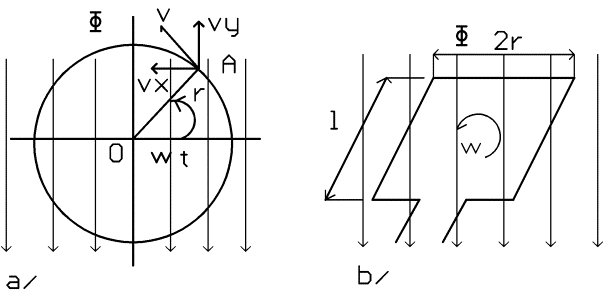
Obrázek a/ . indukce elektrického napětí ve vodiči(w = w)

Obrázek b/. indukce elektrického napětí v závitu(w = w)

u = 2 B l w r sin wt = B S w sin wt, kde

S = 2 r l je plocha závitu

B . S = Ø_max je největší magnetický tok, který závitem prochází v poloze kolmé ke směru magnetického pole.

Okamžitou hodnotu indukovaného napětí vypočítáme ze vztahu   u = w Ø_max sin wt

Maximální indukce napětí nastává, je-li rovina závitu ve směru magnetického pole

w t = π/2           sin wt = 1 a vodič při svém pohybu protíná co nejvíc siločar. Indukované napětí se rovná nule, je-li rovina závitu kolmá na směr magnetického pole           w t = 0, sin wt = 0 a vodič neprotíná žádné siločáry.

 

Fázory

Sinusový průběh odvozujeme z kruhového pohybu. Můžeme si jej představit pomocí orientované úsečky, která rotuje okolo počátku souřadnic proti směru hodinových ručiček. Úhlová rychlost jejího otáčení je totožná s úhlovou frekvencí kmitů w, délka úsečky určuje amplitudu (U_max, I_max) a počáteční poloha úsečky určuje počáteční fázi j.

            Takováto úsečka, které dokonale určuje sinusový průběh, se nazývá fázor (dříve se nazýval časový vektor). Jeho ypsilonová složka určuje okamžitou hodnotu napětí nebo proudu. Pokud rotující úsečku (rotující fázor) zastavíme např. v čase t = 0, získáme statický fázor. Střídavé harmonické veličiny tedy vyjadřujeme pomocí fázorů. Jejich sčítání a odčítání provádíme vektorově, nikoliv pouze algebraicky jako u veličin stejnosměrných. Vektorové sčítání je přehlednější než početní řešení, kdy se sčítají okamžité hodnoty veličin. Vektorově můžeme sčítat pouze střídavé veličiny o stejné frekvenci.

 

Základní elektronické součástky v obvodu střídavého proudu.

Zavedeme pojmy: ideální rezistor – jeho jediným parametrem je elektrický odpor, ideální cívka – jediným parametrem je indukčnost a ideální kondenzátor – jediným parametrem je kapacita.

Ideální rezistor v obvodu střídavého proudu

Na ideálním rezistoru jsou napětí a proud ve fázi, platí Ohmův zákon

u = U_max sin wt  i = I_max sin wt = (U_max/R) sin wt             R = u/i = U_max/I_max = U/I

Ohmův zákon platí pro okamžité, maximální a efektivní hodnoty proudu a napětí.

 

Cívka v obvodu střídavého proudu.

Pokud připojíme zdroj střídavého napětí sinusového průběhu k ideální cívce, bude cívkou procházet sinusový proud. Ten vybudí magnetický tok Ø, který je ve fázi s proudem i.

            Magnetický tok indukuje v cívce napětí, které je přímo úměrné změně proudu za jednotku času a indukčnosti cívky L.                        u_L = L di/dt

Jedná se o velmi důležitý vztah mezi proudem a napětím na cívce. Matematicky (pomocí derivací) u něj můžeme odvodit všechny vlastnosti ideální cívky (vzorec pro indukční reaktanci,.napětí předbíhá proud o 90°, přechodový děj při připojení do obvodu, apod)

            Indukované napětí je tím větší, čím větší je změna proudu. Při průchodu proudu nulou bude proto napětí maximální. Roste-li proud, bude napětí kladné. Je-li proud maximální, bude napětí nulové. Klesá-li proud, bude napětí záporné.

            To znamená, že napětí předbíhá proud o π/2 (90°). (Nejprve na cívku přivedeme napětí, které vytvoří magnetické pole, potom začne procházet proud.) Platí zákon, že indukované napětí působí svými účinky proti změně, která jej vyvolala (Lencův zákon). To znamená, že ačkoliv ohmický odpor cívky je při stejnosměrném proudu nulový, střídavému proudu klade cívka „odpor“, kterým je proud omezen. Tento odpor je pouze zdánlivý a nazývá se indukční reaktance X_L [Ω]

Platí U_max = I_max . X_L, U = I . X_L.

Tento vztah vyjadřuje Ohmův zákon pro obvod s ideální cívkou.

Indukční reaktanci vypočítáme ze vztahu X_L = wL = 2πfL.       Dosazením jednotek si můžeme ověřit, že její jednotkou jsou ohmy. Jedná se o veličinu frekvenčně závislou. Indukční reaktance X_L roste lineárně s frekvencí, proud tekoucí cívkou je nepřímo úměrný frekvencí.

Převrácenou hodnotou indukční reaktance je indukční susceptance, značíme ji B, jednotkou je siemens.

Jalový výkon

Okamžitý výkon střídavého proudu v ideální cívce získáme vynásobením okamžitých hodnot napětí a proudu.                              p = u . i

Okamžité hodnoty výkonu jsou kladné nebo záporné, protože napětí a proud jsou fázově posunuté o 90°.

            Kdybychom toto násobení provedli bod po bodu v celé periodě, zjistili bychom, že výkon v cívce kmitá s dvojnásobnou frekvencí okolo nulové hodnoty. Dochází k výměně energie mezi zdrojem a cívkou. Na cívce se žádný výkon nespotřebovává. Jedná se o jalový indukční výkon, značí se Q. Jeho jednotkou je var (watt reaktanční). Proud, který je zpožděn o 90° za napětím, nazýváme jalový proud (magnetizační proud), který slouží k vytvoření magnetického pole cívky.

Q = U . I

Příklad: Cívka o indukčnosti 0,8 H je připojena k napětí 230 V/50 Hz. Určete proud a jalový výkon

X_L = 2π . 50 . 0,8 = 251,2 Ω                  I = U/X_L = 0,916 A                   Q = U. I = 210,6 (var)

 

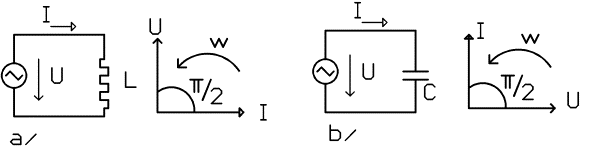
Obrázek:a/ cívka b/ kondenzátor v obvodu střídavého proudu, fázorový diagram (w = w)

 

Ideální kondenzátor v obvodu střídavého proudu.

V stejnosměrném obvodu platí Q = C . U, ve střídavém obvodu ÑQ = C . ÑU

i_C = C . du/dt

Z této rovnice je možné matematicky (derivováním) odvodit všechny vlastnosti kondenzátoru.

            Z této rovnice vyplývá, že čím větší je změna napětí na kondenzátoru, tím větší bude proud kondenzátorem. Při průchodu napětí nulou je maximální proud. Roste-li napětí, má proud kladnou hodnotu. Je-li napětí maximální, je hodnota proudu nulová. Klesá-li napětí je hodnota proudu záporná. To znamená, že v obvodu ideálního kondenzátoru proud předbíhá napětí o π/2. (nejdříve se kondenzátor proudem nabíjí, potom je na něm napětí).

Proud tekoucí kondenzátorem je přímo úměrný jeho kapacitě a provozními kmitočtu „Odpor“ kondenzátoru se nazývá kapacitní reaktance X_c, která se udává v ohmech.

X_c = 1/w C                  U = X_c I

Převrácená hodnota kapacitní reaktance je kapacitní susceptance B = 1/X_c = I/U = wC

            Stejně jako u cívky je okamžitá hodnota výkonu p = u i , má střídavě kladnou nebo zápornou hodnotu a kmitá s dvojnásobnou frekvencí. V obvodu s ideálním kondenzátorem se nespotřebovává žádná energie, dochází pouze k výměně energie mezi zdrojem a kondenzátorem. Energie slouží pouze k vytvoření elektrického pole kondenzátoru. Vzniká jalový kapacitní výkon Q = U . I (var), kondenzátorem prochází jalový kapacitní proud.

Příklad: Jaký proud teče kondenzátorem 100 nF, který je připojen na napětí 230V/50 Hz. Jaký bude jalový výkon?

X_c = 1/(6,28 . 50 . 0,1 . 10^-6) = 31, 84 kΩ

I = 230/31,84 = 7,22 mA = 0,007 22 A

Q = 230 . 7,22 = 1,66 . 10^-3 var

 

Vzájemná indukčnost v obvodu střídavého proudu

 

 

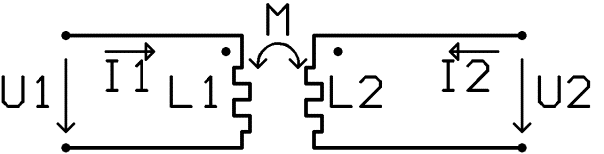
Obrázek: Proudy a napětí v obvodu se vzájemnou indukčností

            Při průchodu střídavého proudu cívkou L₁ se indukuje napětí u₁ = LdI₁/dt

U₁ = I₁ w L₁

V cívce L₂ se indukuje vlivem vzájemné indukčnosti napětí u₂ = M dI₁/dt . Jeho efektivní hodnota je U₂ = I₁ w M

Výraz wM představuje indukční odpor a měří se v ohmech. Napětí v cívkách L₁ a L₂ vytváří stejný magnetický tok. Při stejném smyslu vinutí (označeno na obrázku tečkou) budou obě napětí ve fázi. Bude-li buzena cívka L₂, bude se indukovat napětí v cívce L₁.

            Vzájemná indukčnost cívek může mít znaménko kladné nebo záporné, podle smyslu jeho vinutí a zapojení jeho konců. Vzájemná indukčnost je kladná, pokud se magnetické toky obou cívek sčítají. Pokud se odčítají, je vzájemná indukčnost záporná. Vzájemnou indukčnost využíváme nejčastěji v transformátorech. Výše uvedenou zákonitost můžeme snadno ukázat v praxi. Máme-li např. transformátor se dvěma sekundárními vinutími 10 V a 2 V. Můžeme je spojit do série dvěma způsoby. Jednou získáme součet napětí (12 V), při druhém způsobu jejich, rozdíl (8 V). Umístění dvou cívek na společné jádro mnohonásobně zvětší jejich vzájemnou indukčnost, protože téměř veškerý magnetický tok prochází jádrem. Jeho permeabilita mnohonásobně převyšuje permeabilitu okolního prostředí.

 

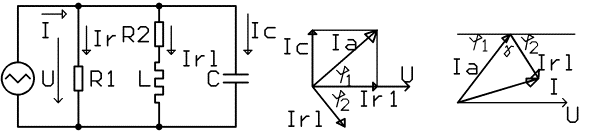
Složené obvody R, L, C v obvodu se střídavým proudem

V obvodech R, L, C platí oba Kirchoffovy zákony. Jediný rozdíl je, že součet proudů v uzlu a součet napětí ve smyčce provádíme vektorově, protože se jedná o fázory

K jejich  řešení používáme fázový diagram.

 

Sériový obvod RL

 

 

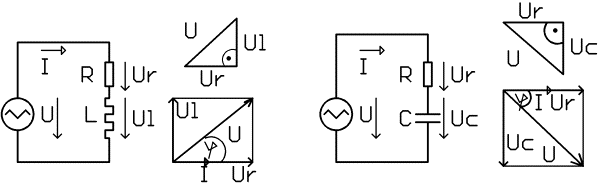
Obrázek: Schéma zapojení sériového obvodu R L (vlevo) a sériového obvodu RC(vpravo)

             

            Rezistorem a cívkou prochází stejný proud, který je ve fázi s napětím U_r. Napětí na cívce U_L předbíhá proud o 90°.

Fázor U_R a U_L vektorově sečteme. Výsledné napětí U s nimi tvoří pravoúhlý trojúhelník. Jeho velikost vypočítáme řešením tohoto trojúhelníka pomocí Pythagorovy věty.

U = I . Z, kde Z je impedance obvodu, která se udává v ohmech. Její charakter je částečně odporový, částečně indukční Z² = R² + X_L²

Fázový posun j mezi celkovým napětím a celkovým proudem vypočítáme z trojúhelníku napětí

Vydělíme-li napětí U, U_r a U_L proudem, získáme trojúhelník impedancí. Není třeba se učit zpaměti všechny vzorce týkající se tohoto i dalších obvodů. Stačí si zapamatovat fázový diagram a umět vyřešit příslušný trojúhelník.

            Sériový obvod RL je mimo jiné náhradním schématem skutečné cívky. Každé vinutí má určitý činný odpor, který představuje veličina R.

Příklad: V sériovém obvodu, kde R = 100 Ω a L = 0,5 H stanovte jeho impedanci, úhel fázového posunu mezi proudem a napětím. Jak velký proud poteče obvodem při napětí 230 V/50 Hz?

Z² = R² + X_L²               Z = 186 W        I = U/Z = 1,23 A

tg j = X_L/R = 157/100 = 1,57                j = 57,5°

 

Sériový obvod RC

Obdobně jako v předchozím případě sčítáme U_c a U_R vektorově, proud tekoucí obvodem je na obou součástkách stejný a je ve fázi s napětím U_R.

Napětí U_R, U_C, a U tvoří pravoúhlý trojúhelník, který řešíme pomocí Pythagorovy věty

Proud předbíhá napětí o úhel j , který je větší než 0° a menší než 90°. Obvod má kapacitní charakter.

Příklad: Kondenzátor 220 nF je v sérii s rezistorem 2 kΩ. Jak velký poteče obvodem proud, připojíme-li jej k napětí 230 V/50 Hz. Jak velké bude napětí na rezistoru?

Xc = 1/(2 . p . f .C) = 1 / (6,28 . 50 . 0,22 . 10^-6) = 14,5 kW       Z = Ö(14,5² + 2²) = 14,63 kW

I = U/Z = 15,72 mA                  U_r = R I = 15,72 . 2 = 31,44 V

Kondenzátor podobné kapacity (dimenzovaný na napětí minimálně 400 V, raději na 630 V) bývá často zapojován v obvodech přímo napájených ze sítě (bez transformátoru) namísto rezistoru. Místo rezistoru může být zapojen i složitější elektrický obvod. Kondenzátor omezuje napájecí napětí tohoto obvodu. Jeho výhodou je, že se nezahřívá, nevznikají na něm žádné tepelné ztráty.

 

Sériové spojení LC – ideální sériový rezonanční obvod.

Oběma prvky prochází stejný proud. Napětí na cívce předbíhá tento proud o 90°, napětí na kondenzátoru se za tímto proudem o 90° zpožďuje. U_L a U_C jsou proto v protifázi, jejich hodnoty se odečítají.

            Impedance obvodu Z = (X_L – X_C) má pro X_C > X_L kapacitní charakter a pro X_C < X_L  indukční charakter.

            Pro X_L = X_C dochází k rezonanci, impedance obvodu je nulová. Nyní si odvodíme výpočet rezonančního kmitočtu

X_L = X_C           wL = 1/wC        w² = 1/LC         f = 1 / (2pÖ(LC)) Thomsonův vzorec

 

Skutečný rezonanční obvod

Jak jsme si již uvedli, ideální cívka neexistuje, každá indukčnost obsahuje i činný odpor.

 

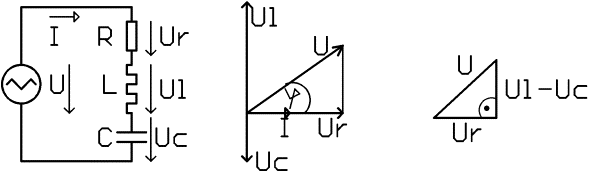
Obrázek: Sériový obvod RLC

Proto žádný rezonanční obvod nemůže mít nulovou impedanci. Z² = (X_L - X_C)² + R²

V rezonanci, kdy X_C a X_L se odečtou bude Z = R. Poměr X_L/R nebo X_C/R udává jakost rezonančního obvodu, kterou označujeme písmenem Q.

 

Příklad: Jaký je rezonanční kmitočet sériového spojení L = 2,2 mH a C = 15 nF?

f = 1 / (6, 28 . Ö(2.2 . 10^-3 . 15 10^-9)) =  1 / (6,28 Ö(33 . 10^-12)) = 1/(36.10^-6) = 27,77 kHz

 

Příklad: Cívka z předcházejícího příkladu má činný odpor 10 ohmů. Jaký bude proud tekoucí obvodem, při rezonanci, je-li U = 0,5 V. Jaký bude činitel jakosti obvodu?

Z = R = 10 Ω               I = U/R = 0,05A = 50 mA

X_L = 2pfL = 6,28 . 27,77 .10³ . 2,2 . 10^-3 = 383,6 W

Q = X_L / R = 383,6/10 = 38,36

 

Všimněte si, že proud tekoucí sériovým rezonančním obvodem je poměrně velký. Zkuste si vypočítat impedanci obvodu pro různé kmitočty (1 kHz, 10 kHz, 20 kHz, 25 kHz, 30 kHz, 40 kHz, 60 kHz) a výsledek graficky znázornil. Získáte tak rezonanční křivku tohoto obvodu. Zjistíte, že rezonanční obvod výrazně potlačuje kmitočty v okolí rezonance. Využívá se v radiotechnice jako odlaďovač kmitočtu.

 

Příklad: Sériový obvod RLC, R = 5 Ω, C = 150 nF, L = 12 mH připojíme ke generátoru s proměnným kmitočtem a  stálou amplitudou 1V.

            Jaký kmitočet musíme nastavit, aby byl obvod v rezonanci? Jaký proud obvodem poteče při rezonanci a jaké bude napětí na jednotlivých prvcích obvodu?

f_r = 1 / 6,28 Ö( 150 . 10^-9 . 12 . 10^-3) = 1 / 6,28 Ö(1800 . 10^-12) = 1/(266,4 . 10^-6 ) = 3,753 kHz

Z_rez = R = 5 Ω              I = U/Z = 1/5 = 0,2 A               U_r = R . I = 1 V

U_L = X_L . I = 56, 56V               U_C = X_C . I = 56, 56 V

 

Povšimněte si, že rezonanční napětí na cívce a na kondenzátoru je mnohem větší (Q krát) než napájecí napětí rezonančního obvodu. Kondenzátor musí být na toto napětí dimenzován.

            Zkuste vypočítat impedanci tohoto obvodu pro kmitočet nižší než je rezonanční kmitočet, ověřte, že X_L bude větší než X_C a proud bude menší než proud v rezonanci. S rostoucí vzdáleností od rezonančního kmitočtu se bude zmenšovat U_C a U_L.

 

Paralelní obvod RC

Dva paralelně spojené prvky mají vždy stejné napětí. Proudy, které jimi procházejí sčítáme jako fázory (vektory) – Impedanci obvodu vypočítáme podle vzorce

I_r = U/R                       I_C = U/X_C

I² = I_R² + I_C² z trojúhelníku proudů vypočítáme I

Z = U/I

 

Příklad: Ke zdroji střídavého napětí 24 V/50 Hz připojíme kondenzátor 8 mikrofaradů a rezistor 600 ohmů. Určete impedanci obvodu, celkový proud a fázový posun mezi proudem a napětím.

I_R = 24/0,6 = 40 mA                 I_C = 24/6,28 . 50 . 8 . 10^-6 = 24 /( 2,512 . 10^-3 ) = 9,55 mA

I² = 1 691                     I = 41,1 mA                  tg j = I_C/I_R = 0,238                  j = 13,42°

Většina proudu teče přes odpor, obvod má pro tento kmitočet spíše odporový charakter.

 

Paralelní obvod RL

            Stejně jako na paralelním obvodu RC je na obou prvcích stejné napětí. Nejprve vypočítáme proudy I_R = U/R a I_L= U/(2pfL), z trojúhelníku proudů pomocí Pythagorovy věty vypočítáme celkový proud I. Stejným způsobem vypočítáme celkovou impedanci a fázový posun mezi proudem a napětím. Z = U/I                tgj = I_L/I_R

 

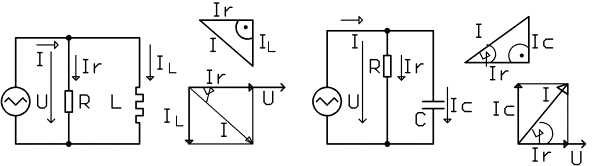
Obrázek a/  Paralelní obvod RL         b/  Paralelní obvod RC

 

Příklad: Paralelní obvod R = 30 Ω, L = 60 mH připojíme k napětí 120 V/100 Hz, Vypočítejte proud tekoucí obvodem a fázový posun mezi proudem a napětím.

I_R = 120/30 = 4 A         I_L = 120/(6,28 . 100 . 60 . 10^-3) = 120/37,68 = 3,18 A

I² = 4² + 3,18² = 26,11   I = 5,11 A        

Z = 120/5,11 = 23,48 Ω             j = arctg I_L/I_R = arctg 3,18/4 = 38,45°

Upozornění: Paralelní obvod RL není nikdy ideální. Každá cívka má určitý činný odpor. Cívku ale nikdy nepřipojujeme paralelně ke zdroji napětí se stejnosměrnou složkou (chová se jako zkrat)

 

Paralelní obvod RLC (paralelní rezonanční obvod)

Všechny prvky jsou připojené na stejné napětí. Celkový proud je součtem dílčích proudů

Proud I_C a I_L jsou vzájemně posunuty o 180°. Jejich účinek se ruší, proudy se odečítají.

I_R = U/R          I_C = U/X_c = U w C        I_L = U/X_L = U/wL

Výsledný proud vypočítáme z trojúhelníku proudů podobně jako v předchozích dvou zapojeních   I² = I_R² + (I_C – I_L)²

Stejným způsobem vypočítáme i celkovou impedanci obvodu a fázový posun mezi proudem a napětím.    Z = U/I  

Příklad: Paralelní rezonanční obvod R = 500 Ω, L = 5 mH, C = 220 nF připojíme ke generátoru s výstupním napětím 2 V o kmitočtu f = 2 kHz. Vypočítejte proud tekoucí obvodem a fázový posun mezi tímto proudem a napětím

 

X_L = wL = 6,28 . 2 . 10³ . 5 . 10^-3 = 62,8 Ω                     I_L = 2/62,8 = 0,0318 A = 31,8 mA

I_R = U/R = 2/0,5 = 4 mA

X_C = 1/wC = 1/(6,28 . 2 . 10³ . 0,22 . 10^-6) = 5,52 . 10^-3A = 5,52 mA

I² = I_R² + (I_L - I_C)² = 4² + (31,8 – 5,52)² = 16 + 704 = 720                      I = 26,8 mA

tgj = (I_L - I_C)/I_r = 31,8 - 5,52/4 = 6,57               j = 81,3°

Výše uvedený obvod se při tomto kmitočtu chová jako obvod RL, říkáme, že má indukční charakter. Při vyšších kmitočtech potečevíce proudu kondenzátorem, obvod bude mít kapacitní charakter. Můžete si to vyzkoušet, proveďte výše uvedený výpočet i pro jiné kmitočty.

Obdobně jako u sériového RLC obvodu i u paralelního rezonančního obvodu dochází při určitém kmitočtu k rezonanci. Má-li indukčnost i kapacita stejnou impedanci, bude X_C = X_L a I_C = I_L a obvodem poteče pouze proud I_R. Impedance obvodu bude maximální a bude rovna R. Vzorec pro rezonanční kmitočet odvodíme stejným způsobem jako u sériového rezonančního obvodu f_rez = 1 / (2pÖ(LC)).

            Tento obvod se používá v radiotechnice všude tam, kde potřebujeme z velkého množství signálů jeden vybrat a ostatní potlačit.

Příklad: U obvodu s předcházejícího příkladu vypočtěte rezonanční kmitočet a proud jednotlivými prvky při rezonanci.

f_rez = 1 / (2pÖ(LC)) = 1/(6,28Ö(5.10^-3 . 220.10^-9)) = 1/6,28Ö(1100 . 10^-12) = 1/(208 . 10^-6) = 4,8 kHz

 

U paralelního rezonančního obvodu nastává tzv. proudová rezonance. Přes obvod teče pouze činný proud (kdyby byl R nekonečný, byl by proud nulový a impedance by byla nekonečně velká). Cívka a kondenzátor si navzájem vyměňují energii prostřednictvím proudů  I_C a I_L. Tyto proudy jsou Q krát větší než celkový proud. Činitel jakosti Q můžeme vypočítat ze vztahu Q = R/2π f_rL nebo Q = R / 2πf_rC. Udává, kolikrát je při rezonanci impedance odporu větší než impedance cívky nebo kondenzátoru.

 

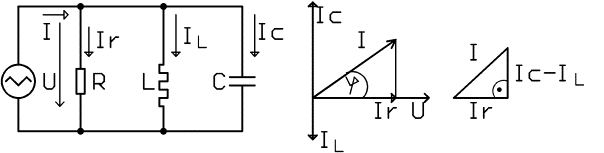
Obrázek: Paralelní rezonanční obvod a jeho fázový diagram.

 

Skutečný rezonanční obvod

Již jsme si vysvětlili, že skutečná cívka má kromě indukčnosti i činný odpor (viz obrázek níže).

Při rezonanci platí vztah

I_RL = I_C                jaková složka proudu I_RL = I_C     I_C = wCU

Odvozením - viz[2] - získáme vztah:      w_r² = 1/(LC) -R²/L²

Člen (R/L)² obvykle bývá zanedbatelný, jeho vynecháním dostaneme původní tvar Thomsonova vzorce. Snížení rezonančního kmitočtu vlivem ztrát na cívce je ve většině případů zanedbatelné.

 

Řešení složitějších RLC obvodů

 

 

 

Obrázek: Obecný obvod RLC a jeho fázorový diagram

Při řešení takovýchto obvodů vypočítáme výše popsaným způsobem nejprve proud I_R =U/R₁, I_C =UwC a I_RL = U/Z, kde Z² = R₂² + (wL)²

Výsledný proud získáme vektorovým součtem těchto proudů. Nejprve sečteme proudy I_R a I_C pomocí Pythagorovy věty, získáme proud I_a =Ö(I_C + I_R)

K sečtení proudů I_a a I_RL musíme umět vyřešit obecný trojúhelník. Máme-li vypočtené úhly j₁ a j₂, můžeme vypočítat úhel g = 180° - (j₁ + j₂) a celkový proud

I_celk = Ö(I_a² + I_RL² – 2I_aI_RLcosg)

Známým způsobem vypočítáme impedanci. Z_celk = U/I_celk

 

Činný a jalový výkon

Připojíme obecný RLC obvod ke zdroji střídavého napětí U, kterým protéká proud I. jje fázový posun mezi U a I. Potom můžeme určit

Činný výkon P = U . I . cos j  [W] 

Jalový výkon P = U . I . sin j  [var]

Zdánlivý výkon P = U . I [VA]

Činný výkon vytváří práci a tepelné ztráty na rezistorech, světelný tok žárovky, pohyb motoru, apod. měříme jej wattmetrem. Výkon je maximální, má-li zátěž čistě odporový charakter a mezi proudem a napětím je nulový fázový posuv. Cos j se nazývá účinník. Tento údaje je často uveden na elektrospotřebičích.

            Jalový výkon vzniká při připojení kapacitní nebo indukční zátěže. Tento výkon si vyměňuje zdroj a zátěž. Vytváří se jím elektrické pole kondenzátoru nebo magnetické pole cívky. Jakový výkon nevykonává práci.

            Zdánlivý výkon vypočítáme z naměřených hodnot proudu a napětí. Udává horní mez výkonu.

            Vztah mezi těmito veličinami udává trojúhelník výkonů, řešíme jej pomocí Pythagorovy věty. S² = P² + Q² = U²I² cosj + U²I sinj = U.I (cos²j + sin²j) = U.I

Příklad: Na štítku motoru jsou údaje: U = 230 V, I = 5 A, cos j  = 0,8. Vypočítejte činný výkon.

P = U. I cos j  = 230 . 5. 0,8 = 950 W

Příklad: Na motoru jsme wattmetrem naměřili 500 W při napětí 230 V. Jaký proud teče obvodem, je-li účiník 0,85?                    I = P/(U . cosj = 500/(230 .0,85) = 2,56 A

            Jaký je činný odpor a indukčnost vinutí  tohoto motoru, f = 50 Hz

P = RI²            R = 76,3 W                   j = arccos 0,85 = 31,78°

Q = U . I . sin j = 310 var        Q = X_L I²         X_L = 47,32 W                L = 0,15 H

 

Příklad: Cívkou stykače teče proud 40 mA. Činný odpor cívky je 3 kΩ. Jaký je činný a jakový výkon cívky při napětí 230 V/50 Hz?

S = U.I = 230 . 0,04 = 9,2 VA               P = RI² = 3.10³ . 0,04² = 3.10³ . 16 . 10^-4= 4,8 W

Q² = S² - P² = 84,64 – 23,04 = 61,6                   Q = 7,85 Var

X_L = Q/I² = 4 905 Ω                 L = X_L/2πf = 15,62 H

S jalovým výkonem se setkáváme hlavně u motorů, protože jejich vinutí má indukčnost. I když jalový výkon nevyvolává tepelné ztráty, musíme se jeho problematikou zabývat. Výměna energie mezi zdrojem (elektrárnou) a spotřebičem (např. motorem) probíhá po vedení, na kterém vznikají zbytečné ztráty. Velkoodběratelé mají proto povinnost kompenzovat jalový výkon (indukční zátěž) přidáním paralelních kondenzátorů. Výměna energie potom probíhá mezi motorem a kompenzačním kondenzátorem.

 

 

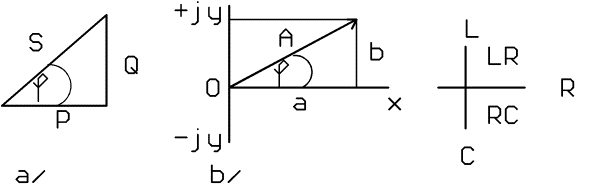
Obrázek: a/ Trojúhelník výkonů                    b/ komplexní rovina, obvody RLC v komplexní rovině          

 

Že budoucnost číslicové techniky patří mikroprocesorům, je každému zřejmé. Procesory PIC patří k nejperspektivnějším, díky jejich jednoduchosti jsou ideální pro výuku. Následující publikace jsou napsány podle zásady, že praxe člověka nejvíc naučí.Po krátkém teoretickém úvodu následují důkladně okomentované programy (digitální hodiny,alarm, měřič rychlosti reakce, čítač), které pochopí i začátečník.

Praktické použití procesoru PIC, (teorie i programy, 56 stran).

 Programujeme PIC (programy s komentářem, 44 stran)

 

Integrovaných obvodů existuje dnes nepřeberné množství. Alespoň trochu se orientovat v této problematice umožňuje publikace Zajímavé integrované obvody (44 stran) –p řevodníky U/f, A/D, D/A, ovládání motorů, fázová regulace výkonu, spínaní v nule, spínané zdroje – konstrukce.

 

Při konstrukci elektrických přístrojů je největším problémem mechanika. Jak  zvládnout bez strojních nůžek a ohýbačky plechu stavbu zdroje, zesilovače, generátoru a čítače ukazuje publikace Elektronické konstrukce pro pokročilé (70 stran). K výše uvedeným konstrukcím dodávám všechny mechanické díly vč. předního panelu se sítotiskem

Další konstrukce: Dekoder Dolby Pro Logic, signalizace telefonních hovorů, zpožděné rozsvícení žárovky, úsporné osvětlení s LED, nf milivoltmetr, akustický spínač

Telekomunikace, informační technika a bezdrátový přenos informací je rozvíjejí závratnou rychlostí (např. mobilní telefony). Jejich principem se zabývám v publikaci Modulace a přenos signálu(69 stran). Analogové a digitální modulace, základy radiotechniky, smyčka PLL, kmitočtová syntéza, digitální ladění, návrh plošných spojů pomocí PC (program EAGLE), nabíjení akumulátorů. Konstrukce: automatický spínač, ochrana čerpadla, zesilovač akustických signálů. Výuková stavebnice SMD.

 

 

Symbolicko-komplexní metoda řešení RLC obvodů

            Řešení obvodů pomocí fázorů, pomocí pravoúhlého nebo obecného trojúhelníka je pro složitější obvody nepřehledné. Každý fázor (každou impedanci) ale můžeme zapsat jako komplexní číslo. S komplexními čísly můžeme provádět všechny aritmetické operace. Komplexní číslo definujeme v Gaussově rovině. Osa x je osa reálných čísel (Re), na ose y jsou čísla imaginární (Im). Imaginární čísla značíme v matematice symbolem i. V elektrotechnice používáme symbol j, protože i zde značí okamžitou hodnotu proudu.

Komplexní čísla byla původně zavedena v matematice, aby bylo možné řešit rovnice typu x² = -1. Platí, že j^-2 = -1, 1/j = -1. Komplexní číslo definujeme v Gaussově (komplexní) rovině. (Reálné číslo je určeno bodem na ose x). Komplexní číslo je jednoznačně uvedeno svou reálnou (x ová souřadnice) a imaginární (y ová souřadnice) složkou. Komplexní číslo má tvar a + j b, tento tvar nazýváme součtový.

Absolutní hodnota komplexního čísla A nám udává vzdálenost jeho obrazu (bodu v komplexní rovině) od počátku souřadnic.

Tuto vzdálenost nazýváme modulem komplexního čísla

Úhel j, který svírá úsečka OA s kladným směrem reálné osy x (měřený proti směru otáčení hodinových ručiček) se nazývá argumentem komplexního čísla.

Komplexní čísla A = a + jb lze psát ve tvaru goniometrickém A (cos j + j sin j) nebo ve tvaru exponenciálním A = A e^jj, kde A² = a² + b²,   j = arctg b/a

Čísla komplexně sdružené k číslu A značíme A^* = a – jb = A e^-jj . Jedná se o číslo, jehož obraz je symetrický k obrazu čísla A podle osy x.

 

Matematické operace s komplexními čísly

Součet (rozdíl) dvou komplexních čísel provedeme, sečteme-li (odečteme-li) zvlášť jejich reálné a imaginární části

A₁ – A₂ = a₁ +jb₁ + a₂ + jb₂ = (a₁ + a₂) + j(b₁ + b₂)

Příklad: Sečtěte A = 2 + 5 j a B = 3 – j

C = A + B = 2 + 5j + 3 - j = 5 + 4 j = algebraický tvar, který můžeme převést na exponenciálné tvar

=Ö(5² + 4²) e^jj = 6 e^j38,65°

Násobení můžeme provádět buď v exponenciálním nebo součtovém tvaru

A₁ – A₂ = (a₁ + jb₁) . (a₂ + jb₂) = a₁a₂ + ja₁b₂ + jb₁a₂ + j²b₁b₂ = a₁a₂ –b₁b₂ +j(a₁b₂ + b₁a₂)- násobení dvou mnoho členů s využitím vztahu j² = -1. Výsledek dále převedeme výše uvedeným způsobem na exponenciální tvar.

Jednodušší je provádět násobení přímo v exponenciálním tvaru A e^ja . B e^jb = A . B e ^j(a+b)

 

Při dělení komplexním číslem vynásobíme čitatele i jmenovatele číslem komplexně sdruženým. Tím se zbavíme komplexního čísla ve jmenovateli.

V exponenciálním tvaru je dělení jednodušší A/B = A/B e ^j(a-b)

 

Mocnina (odmocnina) komplexního čísla (A e^ja)² = A² e^j2a       Ö(A e^ja) =ÖA . e^ja/2

 

Fázory proudu a napětí a impedance RLC obvodů lze vyjádřit ve tvaru komplexních čísel. Impedance rezistoru má pouze reálnou složku, impedance ideální indukčnosti bude mít tvar jwL a bude ležet na kladné části osy y. Impedance ideálního kondenzátoru 1/(jwC) = -j/(wC) bude ležet na záporné části osy y.

V prvním kvadrantu (x > 0, y > 0) budou ležet impedance obvodů RL, ve 4 kvadrantu (x > 0, y <  0) budou ležet impedance obvodů RC. Všechny fázory proudů a napětí, kterými jsme se až dosud zabývali, můžeme zobrazit rovněž jako komplexní čísla a provádět s nimi výše uvedeným způsobem matematické operace.

 

Příklad: Určete impedanci paralelního RC obvodu R = 70 Ω, C = 40 mikrofaradů, f = 50 Hz

Z = R – j/wC = 70 – j/(6,28 . 50 . 40 . 10^-6)= 70 – j/0,0125 = (70 – j 79,6) Ω

Tuto impedanci najdeme v Gaussově rovině ve 4. kvadrantu.

 

Příklad: K napětí, které je vyjádřeno ve tvaru U = 10 + j15 V je připojeno sériový obvod RLC, R = 5 Ω, X_L = 15 Ω, X_C = 20 Ω. Jaký proud prochází obvodem?

U = 18 e^j56°        Z = 5 + j15 – j20 = 5 –5j = 7,05 e^j-45°     obvod má charakter obvodu RC

I = U/Z = 18/7,05 e ^{j 56-(-45) °} = 2,55 e^j101°                                   proud předbíhá napětí

 

Příklad: Jaký proud poteče zadaným obvodem z následujícího obrázku, je-li R₁ = 3 Ω, X_L = 5 Ω, R₂ = 10 Ω, X_C = 5 Ω, připojíme-li k němu napětí 24 V?

Nejprve jsme vypočítáme impedanci paralelního spojení R₂ C (počítá se téměř stejně jak paralelní spojení dvou rezistorů) nejlépe v součtovém tvaru.

1/Z_R2C = 1/R₂ +1/(-jX_C) = 1/R₂ +j1/X_C = 0,1 + j0,2         admitance R₂ paralelně C

Na impedanci převedeme pomocí násobení číslem komplexně sdruženým, abychom odstranili komplexní číslo ze jmenovatele.

Z_R2C = 1/(0,1 + j0,2) = 0,1 – j0,2 / (0,1² +0,2²) = 0,1 – j0,2 /0,05 = 2 –j4

Přičteme k němu impedanci R₁ a L.

Z_CELK = 3 + j5 +2 –j4 = 5 + j

Převedeme na exponenciální tvar          Z_CELK = Ö26 . e^j11,3° = 5,1 . e^j11,3°

I = U / Z_CELK = 24/(5,1 . e^j11,3°) = 4,7 e^-j11,3° obvod má indukční charakter, proud se zpožďuje za napětím.

Všimněte si, že způsob řešení je podobný jako u stejnosměrných obvodů s rezistory. Provádíme-li součet, pracujeme s komplexním číslem v součtovém tvaru. Při násobení a dělení naopak potřebujeme tvar exponenciální.

 

 

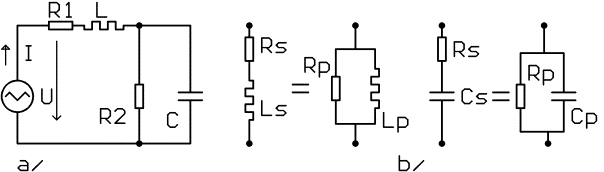
Obrázek: a/ Příklad RLC obvodu       b/ Duální obvody

 

Duální obvody.

            Při řešení elektrických obvodů lze někdy nahradit sériové spojení dvou součástek RC nebo RL paralelním zapojením a naopak.

Duální obvody jsou obvody, které mají při stejné frekvenci stejnou impedanci (modul i fázi). Vztahy pro obvody RL a RC jsou stejné.

Sériovou reaktanci označíme X_S, paralelní X_P, sériový odpor R_s, paralelní odpor R_p

R_S = R_PX_P² / (R_P² + X_P²)         X_S = R_P²X_P / (R_P² + X_P²)

 

R_P = (R_S² + X_S²)/R_S                     X_P = (R_S² + X_S²)/X_S

 

 

Ceník a stručný obsah publikací

Platí do 31.12. 2002. Případné úpravy po tomto datu budou pouze v návaznosti na velkoobchodní ceny (inflace), větší změny nepředpokládám. Nejsem plátcem DPH. V sadě součástek jsou všechny součástky uvedené v seznamu s vyjímkou součástek uvedených v závorce. Případná změna hodnot a typů vyhrazena, pokud nemůže podstatným způsobem ovlivnit vlastnosti a funkci popsaného zapojení. Záruku na součástky neposkytuji.

Poštovné: dle tarifů České pošty.          Balné: do 20,- Kč (u větší zásilky).

Rabat: nad 500 Kč 5%, nad 1000 Kč 10%.

Vlastnosti a užití CMOS obvodů

Základní vlastnosti, vysvětlení jejich funkce na praktických případech, stručný katalog

Výrobek	Plošný spoj	Součástky	Krabička
Poplašné zařízení	78,-	292,-	40,- U-Zi
Časový spínač	57,-	-------	---------
Běžící světlo	37,-	129,-	---------
Měřič kmitočtu	82,-	385,-	59,-  KM33

Zapojení s analogovými obvody

Teorie koncových zesilovačů, parametry OZ, princip stereofonního rozhlasu

Výrobek	Plošný spoj	Součástky	Krabička
Přijímač FM	35,-	192,-
Stereodekodér	39,-	126,-
Zesilovač s LM 386N	27,-	55,-
Melodický zvonek	20,-	76,-
Dálkové ovládání(přijímač)	38,-	248,-
Dálkové ovládání (vysílač)	9,-	35,-	36,- (KM22)
Logická sonda	29,-	198,-	59,- (U-sonda3- s hrotem)
Směšovač (4vst. , 1výstup)	75,-	330,-	40,-(U6)
Mixážní pult(2vst. , výstup)	197,-	690,-	220,-(KP16)
Mixážní pult(2vst.)	132,-	520,-

Měření elektrických veličin         Stručná učebnice měření

Aplikovaná elektronika              Spínané zdroje, OZ v automatizační technice (můstkové zapojení), přehled obvodů HC (HCT) 74 xx, odrušování

Výrobek	Plošný spoj	Součástky
Termostat	43,-	--------
Měřič frekvence	31,-	80,-
Detektor kov. předmětů	23,-	---------
Snímač pohybu	53,-	---------

Elektronika pro hudebníky

Princip syntézy zvuku, příklady zapojení

Výrobek	Plošný spoj	Součástky	Krabička
Metronom	67,-	178,-	46,- (U 6)
9 pás. EQ	78,-	487,-
Mono předzes.	29,-	193,-
Konc. zes. s LM 3886	21,-	476,-
Piánko 15 kláves	43,-	169,-
Booster	38,-	190,-

Trafo 230 /23,  11.5 V,  4W  - 155,-Kč.               Trafo 230/46V,   160W – 720,-Kč

 

Praktické použití procesoru PIC, (teorie i programy)        Programujeme PIC (programy s komentářem)

Výrobek	Plošný spoj	Součástky, vč. napr.proc.
Digit. hodiny	55,-	690,-
Alarm	28,- + 15,- (klávesnice)	460,-
Měřič rychlosti reakce	37,-	470,-
Čítač	74,-	730,-

Naprogramovaný PIC....250,- Kč

Elektronické přístroje (součástky SMD,spínané zdroje, syntéza zvuku, základy regulační techniky, základy elektrotechnologie, TV technika)

Výrobek	Plošný spoj	Sada součástek
Páječka (složitější)	58,-	390,-
Jednoduchý reg. páječky	39,-	195,-
Funkční generátor	62,-	490,-

Pájecí pero PP 530        490,-Kč ,        Pájecí pero CSI 40   195,- Kč         

Stojánek pájecího pera SP 530     170,- Kč

Zajímavé integrované obvody (převodníky U/f, A/D, D/A, ovládání motorů, fázová regulace výkonu, spínaní v nule, spínané zdroje – konstrukce.

Elektronické konstrukce pro pokročilé (vyjde asi  koncem r. 2 001)

Výrobek	Plošný spoj	Sada součástek	Trafo	Př. panel	Chladič	Ost. mech. díly
DPM(pro zdroj 3A a 170 V)	62,-	390,-
Zdroj 3A	116,-	480,-	545,-(90W)	445,-	148,(+125)	185,-
Zdroj 170 V	116,-	640,-	695,-(90W)	445,-	148,(+125)	185,-
Zdroj 1A	39,-	268,-	(330) (30W)	278,-		118-
F. generátor	66,-	548,-	(155)-(4W)	285,-		118,-
Zesilovač (1524+2030)			(330) (30W)	285,-		118,-
předzesilovač sTDA 1524	59,-	228,-
konc.stupeň TDA 2030	36,-	248,-
Předz. pro mgd přenosku	27,-	95,-
Ind. síť. napětí	17,-	93,-
5 místný čítač	81,-	470,-		338,-		118,-
Zabezp. ústředna	174,-	550,- (vč. napr. procesoru)
Zkušební deska OZ	138,-	220,-				46,- (krabička U6)
Zkušební deska digitální	138,-	140,-				46,- (krabička U6)

Další konstrukce: Dekoder Dolby Pro Logic, signalizace telefonních hovorů, zpožděné rozsvícení žárovky, úsporné osvětlení s LED, nf milivoltmetr, akustický spínač

Vysvětlivky: Sada součástek dle rozpisky. Plošný spoj lakovaný nevrtaný bez nepájivé masky. Trafo včetně upevňovacích šroubů, e.p. 4 kV. Přední panel odvrtaný, černý elox, sítotisk.

Pro zdroj 3 A a 170 V chladič 25 x 25 x 219 mm, v závorce příplatek za odvrtání a vyřezání závitů. Ostatní mechanické díly: horní kryt ohnutý do tvaru U neodvrtaný bez  povrchové úpravy, spodní a zadní kryt neohnutý, neodvrtaný, bez povrchové úpravy, přístrojové nožičky, plexi k displeji, profil L na vyrobení úhelníků, všechny šrouby

Pro ostatní konstrukce: Ostatní mech. díly = Al profil U 50 x 50 x 219 mm (který u zdroje 1A slouží jako chladič), profil L na výrobu bočních krytů, 4 přístroj. nožičky, distanční sloupky, šrouby, u čítače plexi k displeji)

Modulace a přenos signálu  (vyjde začátkem r. 2002)Analogové a digitální modulace, základy radiotechniky, smyčka PLL, kmitočtová syntéza, digitální ladění, návrh plošných spojů pomocí PC (program EAGLE), nabíjení akumulátorů. Konstrukce: automatický spínač, ochrana čerpadla, zesilovač akustických signálů. Výuková stavebnice SMD 198,-Kč (plošný spoj +souč).       Dále nabízím:  Katalog GM 2001    80,- Kč    

 

 

Pro začátek je nejvhodnější publikace Konstrukční návody, kde jednotlivá zapojení jsem popsal velmi důkladně. Všem zájemcům o tento obor doporučuji postavit si stabilizovaný zdroj, který bude jistě užitečný při dalších pokusech.

Výrobek	Plošný spoj	Součástky	Krabička
Zdroj s LM 317	39,-	186,-	U6     46,-Kč
Zdroj s L200	82,-	387,-	KM85   88,-Kč
Nabíječ NiCd článků	17,-	-
Blikač s malou spotřebou	9,-	58,-
Generátor	29,-	198,-	U-MONA    18,-Kč
Metronom	29,-	125,-	KM22   36,-Kč
Ozdobný blikač	37,-	99,-
Indikátor + „alarm“	19,-	47,-
Indikátor s 3LED	18,-	48,-
Výkonový stabilizátor	46,-

Trafo 30 W  330,- Kč (s odbočkou a držákem pojistky)

 

Postavit si vlastní zesilovač není nic složitého. Oproti koupi hotového přístroje je zde nejen úspora financí, získané zkušenosti jsou k nezaplacení. Radost z úspěchu dodá chuť k další činnosti. Problematikou elektroakustiky se zabývám v publikacích:

Postavte si zesilovač (33 stran)

Výrobek	Plošný spoj	Součástky	Krabička	Ostatní
Konc. stupeň s TDA 2030	36,-	248,-	KM85   93Kč	Trafo 330,-
Přezdzesilovač. s pas. korekcemi	59,-	228,-
Předzesilovač s TDA1524	39,-	266,-
Stereo ekvalizér (4 pásma)	92,-	394,-
2 pásmová reprosoustava		585
Kvadrofonní adaptor	50,-	315,-	KM 85    93Kč	Trafo 330,-

Doplňky nf zesilovače (34stran)

Stereo ind. s 2barevnou LED	19,-	78,-
Indikátor se 4nás OZ - mono	29,-	86,-
Barevná hudba	37,-	159,-
Směšovací jednotka (4 vstupy	174,-	692,-	SB1    159Kč
Konc zesilovač 2x50 W	56,-	392,-	KM85  93Kč	Trafo160W
Usměrňovač a filtr ke konc. stupni	29,-	375,-
Časový spínač	37,-	95,-		Relé 56,-
Měřič rychlosti reakce	28,-	96,-

Trafo 160 W  720,- Kč, trafo 300 W   1190,- Kč

 

Cenník publikácií:

 

Konstrukční návody                        71,- SK

Postavte si zesilovač                          71,- Sk

Doplňky nf zesilovače                          71,- Sk

Zapojení s analogovými obvody             71,- Sk

Elektronika pro hudebníky                 71,- Sk

Vlastnosti a užití CMOS obvodů            71,- Sk  

Aplikovaná elektronika                    101,- Sk

Kurz základů elektroniky                  86,- SK

Měření elektrických veličin               71,- Sk  

Základní elektronické obvody a zařízení   71,- Sk

Aplikace moderních IO                          71,- Sk

Vlastnosti a použití procesoru PIC        86,- Sk

Programujeme PIC                               71,- Sk

Elektronické přístroje                    129,- Sk

Zajímavé integrované obvody          vyjde v nejbližší době

Elektronika pro pokročilé            vyjde v nejbližší době

Modulace a přenos signálu            vyjde začátkem r. 2002

Dále distribuuji ke všem výše uvedeným konstrukcím plošný spoj, sadu součástek, případně další díly (krabička, trafo.

Adresa: Ing. Jiří Vlček, Tehov 122,  251 01 Říčany u Prahy

tel. zam. 02 / 66 107 687, domů 0204/ 64 15 63, mob. 0603 71 99 78

E: vlcek-j zavináč seznam.cz

 

Slovensko:

 

ANIMA

Tyršovo nábrežie 1 (Hotel Hutník)

040 01 Košice

 

tel.: 055/600 3225               e-mail: anima@dodo.sk