TRANSFORMÁTOR JEDNODUŠE

Zde uvedený zjednodušený výpočet silového transformátoru umožňuje snadno a jednoduše určit potřebný průřez jádra, počty závitů jednotlivých vinutí a průměr použitého vodiče. Jistě všichni víte, že u nás (a ve všech státech Evropy) je síťové napětí (tedy to, co máme v zásuvce) 230 V s kmitočtem 50 Hz. Při svých cestách do zahraničí se můžete setkat například ve Spojených Státech s napětím 110, 120 až 220 V s kmitočtem 60 Hz a poněkud jinak řešenými zásuvkami.

Pro napájení tranzistorových zařízení potřebujeme většinou stejnosměrné napětí 9 až 15 V (vyjímečně i jiné), popisy usměrňovačů a stabilizátorů napětí najdete také na tomto webu. Pro elektronková zařízení (ale ty začátečníci asi nebudou stavět) potřebujeme pro napájení větší napětí, kolem 150 až 300 V a také střídavé napětí 6,3 V (dříve i 4 V) pro žhavení elektronek. Všechny tyto napětí, jedno pro jaké zařízení, získáváme z jednoho transformátoru, který se nazývá síťový (nebo také silový).

Síťový transformátor má za základ jádro skládané z plechů ze speciální oceli s příměsí křemíku, obvykle ve tvaru podle následujícího obrázku.

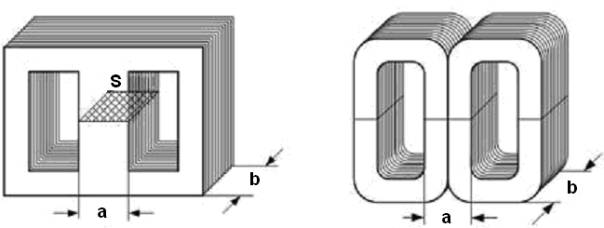
Jeho rozměry, a hlavně plochu průřezu jádra určíme dle požadovaného součtu všech výkonů které má transformátor dodávat svým spotřebičům.

Zjednodušený výpočet začíná zjištěním potřebného průřezu jádra S v cm² který by zajistil potřebný výkon transformátoru.

Tak například, transformátor se středním jádrem o stranách 3 x 2 cm, tedy s průřezem 6 cm², může dodávat výkon až 36 W. Obráceně z tohoto můžeme odvodit, že při požadovaném výkonu pro napájení zařízení 36 W, jednoduše pomocí odmocniny zjistíme, že průřez jádra by měl být 6 cm² .

Takto zjednodušený výpočet dává vcelku uspokojující výsledky, o které se v amatérské praxi můžeme spolehlivě opřít. Je ale mou povinností upozornit na to, že vypočtený průřez jádra je minimálně použitelný, z důvodu magnetického sycení. Takže je možno (a také vhodné) použít jádro s poněkud větším průřezem než vypočteným, dejme tomu namísto výše uvedeného průřezu 6 cm² klidně použijeme jádro s průřezem 8 cm²  nebo dokonce 10 cm² . Jádro s menším, než vypočteným průřezem nepoužívejte, protože pak se jádro dostane do oblasti nasycení, vinutí má nižší induktivní reaktanci, proud bude narůstat a transformátor se bude přehřívat, až může dojít i k přerušení vinutí, „spálení“.

Síťový transformátor má několik vinutí. Za prvé je to primární vinutí, které připojujeme k napájecí síti 230 V, nebo taky jinam – prostě to vinutí, do kterého přivádíme napětí.  Dále je zde jedno nebo více vinutí, zvaných sekundární, to jsou ty vinutí, ze kterých odebíráme napětí (a samozřejmě i proud) ke zpracování, do dalších zařízení. Vstupní a výstupní napětí transformátoru závisí na počtu závitů příslušného vinutí. Abychom mohli určit, kolik závitů má mít to které vinutí, zavedeme si jednotku „závitů na volt“, tedy Z1V. Tento údaj závisí na materiálu jádra a jeho průřezu, orientačně podle následujícího vzorce:

Takže v případě, že podle výše uvedeného příkladu použijeme jádro o průřezu 6 cm² tak podle tohoto vzorce nám vychází v průměru 10 závitů na volt.

Nyní si určíme počet závitů primárního vinutí podle vzorce

a podle něj zjistíme, že pro napájecí síťové napětí 230 V potřebujeme navinout 2 300 závitů. Obdobně určíme počet závitů sekundárního vinutí:

Budeme například vycházet z požadavku výstupního napětí 20V, čili navineme 240 závitů.

Dále ještě potřebujeme zjistit, jaký průměr vodiče pro dané vinutí použít. Pro vinutí transformátorů se používá měděný vodič se smaltovou, nebo lakovou izolací. Při stanovení jeho průměru vycházíme z proudové zatížitelnosti a malých ztrát energie v transformátoru:

 

Jaký bude proud sekundárního vinutí, máme v zadání, takže sílu vodiče pro toto vinutí můžeme spočítat snadno podle výše uvedeného vzorce. Poněkud (ale jen malinko) komplikovanější je určit proud primárního vinutí. Pro přibližný odhad můžeme uvažovat, že kolikrát větší napětí, tolikrát slabší vodič. Ale přeci jen raději použijeme následující vzorce pro výpočet pomocí výkonu a příkonu.

Takže nejprve si určíme výkon sekundáru:

Z něj si odvodíme příkon primáru:

No a určit proud primáru je pak naprosto jednoduché:

A JE TO.