Polovodičové kondenzátory.

 

Nemáte k dispozici vhodný ladicí kondenzátor pro svůj právě konstruovaný přijímač? Žádný problém, použijte diodu!

 

Kondenzátory, založené na změně kapacity polovodičového přechodu P-N nemají příliš velkou jakost (mimo specielně k tomuto účelu vyrobených varikapů), ale v kombinaci s pevnými kondenzátory, pokud charakteristika C=f(U_L) se neuplatní příliš velká, není to zase tak hrozné.Výhodou je jednoduchost změny kapacity čistě elektrickou cestou, pouze změnou napětí, přičemž potenciometr je dostupnější než ladicí kondenzátor s vhodnou kapacitou, a také má o něco větší úhel otáčení, čímž se ladění zjemní. No a více či méně vhodných diod je ve starých zařízeních dostatek, ani není třeba je kupovat. Přitom není nutností použít specielní kapacitní diodu (varikap), pro amatérskou potřebu naprosto vyhoví libovolná plošná Si dioda, já osobně s úspěchem používám Zenerovy diody, kterých je ve vyřazených počítačích dost, navíc mají větší rozsah změny kapacity.

 

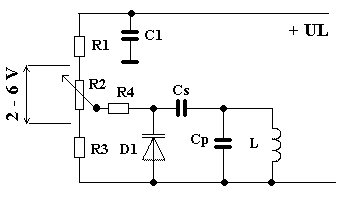
Schema zapojení pro měření závislosti kapacity diody na napětí je na obrázku.

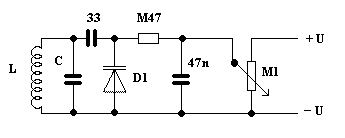
Základem je paralelní laděný obvod LC, jehož rezonanční kmitočet je možno jednoduše zjistit pomocí dipmetru. Použijeme cívku, jejíž indukčnost známe, pro rozsah krátkých vln, který nás zajímá, použijeme cívku s indukčností kolem 1 – 10 mH, ,přičemž s menší cívkou a větším kondenzátorem docílíme větší rozsah přeladění, jak si můžete jednoduchým způsobem sami ověřit. Pro hloubavější povahy doporučuji podívat se do vhodné literatury na další podrobnosti, třeba jak se mění činitel jakosti obvodu Q se změnou poměru L/C.

 

Přiklad:

Pro pokusy použijeme cívku s indukčností 1mH a ladicí kondenzátor 10 – 100 pF.

f = 159 / Ö C * L    (hodnoty samozřejmě vkládáme v MHz, pF, mH)

tedy f = 159 / Ö 10 pF * 1 mH  = 50,28 MHz

a  f = 159 / Ö 100 pF * 1 mH  = 15,9 MHz

Obdobně pro tentýž ladicí kondenzátor, ale s cívkou 50 mH je změna kmitočtu 7,1 – 2,2 MHz, tedy v mnohem menším rozsahu. Podrobněji na toto téma je se můžete dočíst v článku LADĚNÉ OBVODY 1

 

Jo, to bychom měli. Ale co teď? Jak takovou cívku vyrobit? Sledujte dále.

 

Cívky.

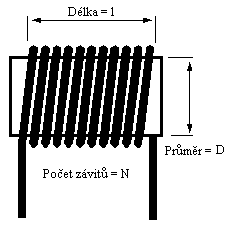
Indukčnost jednovrstvé válcové cívky, tedy takového tvaru, jaký budeme nejvíce používat, se vypočítá podle vzorce

L = r² * N² / (23 * r) + (25 * l)

kde L=indukčnost cívky v mH, r=poloměr vinutí v cm, N=počet závitů a l=délka vinutí v cm, viz obrázek 4, z čehož si snadno můžeme odvodit, že

N = Ö ((23 * r) + (25 * l) * L) / r²

 

Stává se dosti často, že se nám dostane do ruky nějaká hotová cívka (třeba z rozebíraného zařízení), ale její indukčnost právě nevyhovuje. Pak můžeme s úspěchem použít vzorec pro převíjení cívek, který je jednodušší:    N₂ = N₁ * (Ö L₂ / L₁),     kde L₁ = původní indukčnost, L₂ = požadovaná indukčnost (v mH),  N₁ = původní počet závitů a konečně N₂ = kolik závitů je nutno navinout pro dosažení požadované indukčnosti.

 

Při použití cívky s jádrem závisí indukčnost na součiniteli materiálu jádra. Pokud jej neznáme, nezbude, než na kostřičku s testovaným jádrem pokusně navinout například 10 – 20 závitů, paralelně k cívce připojit kondenzátor se známou kapacitou z rozsahu od desítek do stovek pF (k menší cívce menší, k větší třeba až 470 pF), pomocí Dipmetru změřit rezonanční kmitočet, no a pak jednoduše podle nám již známého vzorce L = 25330 / f² * C  (MHz, mH, pF) zjistit její indukčnost. Postup měření Dipmetrem je velice jednoduchý, pro začátek se můžete poradit se zkušenějším kolegou, no a v nejbližší době si budete moci přečíst, jak Dipmetr postavit a naučit se s ním pracovat.

 

Uvádím příklady z praxe, jak jsem měřil indukčnosti já:

Použita kostřička průměru 6 mm (tedy poloměr r = 0,3 cm), navinuto 25 závitů na délku 2 cm. Podle výpočtu by měla mít indukčnost 0,988 mH (naměřená skutečnost 1,04 mH). Nejprve jsem do cívky našrouboval prastaré jádro z práškového železa, a s paralelním kondenzátorem 56 pF jsem naměřil rezonanci na 15,1 MHz, indukčnost tedy byla 1,98 mH. Pak jsem zkusil feritové jádro se zeleným označením a naměřil jsem rezonanční kmitočet 12,3 MHz, indukčnost tedy byla 2,989 mH. Z výsledku jsem si podle vzorce k = N / ÖL zjistil, že konstanta indukčnosti tohoto jádra je 14,46. Nyní pro počet závitů požadované indukčnosti k danému jádru jednoduše:

N = k * ÖL

Tak například potřebuji indukčnost 5 mH:

N = 14,46 * Ö 5 = 32,33 = navinu tedy přibližně 34 závitů a jádro poněkud vyšroubuji.

Takže – je to jasné? Sláva, můžeme tedy pokračovat.

 

Přes oddělovací kondenzátor s menší kapacitou (pokud možno přesně změřenou, zde použita hodnota 33 pF) je připojena měřená dioda. Při zkouškách jsem použil různé typy Zenerových diod, které mají mnohem větší kapacitu, než běžné varikapy. Na milimetrový papír si na vodorovnou osu vyneseme napětí, nastavené potenciometrem M1 a na svislou osu budeme značit kapacitu měřené diody. Nezapomínejte, že kapacita, připojená k cívce L se skládá z kondenzátoru C, a k němu paralelně připojené sériové kombinace kapacit 33 pF a C_D1. Kondenzátor C volíme tak, aby nám s danou cívkou rezonoval co nejblíže kmitočtu, který pak budeme používat (buď výpočtem, nebo odhadem – pro 1 MHz kolem 300 pF, pro 30 MHz kolem 10 pF, pro kmitočty mezi tím interpolujeme).

 

Potenciometrem nastavíme okrouhlou hodnotu napětí na diodě, např. 1V, 2V .... 8V atd., pro každý údaj změříme dipmetrem rezonanční kmitočet. Pak si vypočteme dle známé hodnoty indukčnosti použité cívky celkovou hodnotu kapacity,

 

C_a = 25330 / f² * L   ( hodnoty v pF, MHz, mH)

 

 odpočítáme kapacitu C,

 

C_b = C_a – C

 

Tato výsledná kapacita se skládá ze sériově spojených kapacit C_D1 a pevného kondenzátoru, t.j. v tomto případě 33 pF.

 

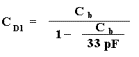
Do mřížky zakreslíme výslednou křivku změn kapacity diody D1.

 

Příklad měření ZD (neznámý typ, bez označení, U_stab = 11,2 V):

 

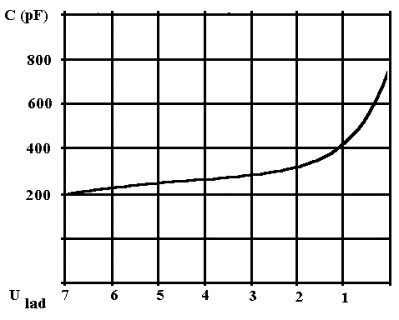
No a již si můžeme vybrat úsek křivky s požadovanou změnou kapacity, např. 2 – 6 V nám dá kapacitu přibližně 220 až 320 pF, se kterou již můžeme počítat do projektovaného laděného obvodu, což nám bohatě pokryje třeba i celé 80m pásmo.

Ladicí potenciometr R2 pak doplníme dvěma odpory R1 a R3 ve funkci děliče, které nastaví požadovaný rozsah ladicího napětí na potenciometru, například na uvedených 2 – 6 V. Odpor R4 s hodnotou řádově stovek kW slouží k oddělení laděného obvodu od potenciometru, který by mohl laděný obvod tlumit. Kondenzátor C1 s hodnotou kolem 10n – M1 nám odfiltruje případné vysokofrekvenční napětí, aby se nemohlo dostat na laděný obvod, nebo z něj do zdroje ladicího napětí. Kondenzátory Cs a Cp volíme podle výše uvedených vztahů.

 

Výpočet odporového děliče napětí je úloha z fyziky na základní škole, pro ty, kteří zrovna ten den chyběli, připomínám:

 

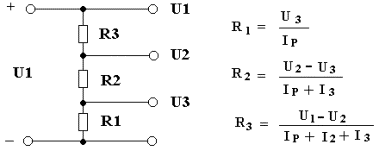
kde I_P je příčný proud děličem. Čím jej zvolíme vyšší, tím tvrdší je výstupní napětí děliče. Pro naší potřebu, kdy z děliče odebíráme jen opravdu minimální proud, není třeba jej volit zbytečně velký, tím se zase zbytečně zatěžuje napájecí zdroj a zhoršuje se stabilizace, úplně postačí kolem 1 – 5 mA.

 

Vstupní napětí pro ladění U_L je výhodné stabilizovat, aby nedocházelo ke změnám kmitočtu vlivem změn napětí způsobených proměnlivým zatížením zdroje. Návrh stabilizátoru napětí se Zenerovou diodou je opět velejednoduchý:

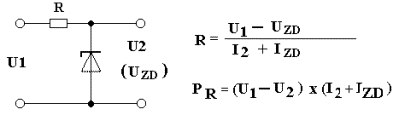
Hodnoty U_ZD a I_ZD si najdeme v katalogu, případně (u neznámých typů ZD) změříme napětí U_ZD  přičemž I_ZD  volíme tak, aby se dioda nepřehřívala, u středních typů (v pouzdrech typu KZ721 – KZ726) kolem 3 – 5 mA, u miniaturních typů kolem 1 mA.

 

Potřebná změna kapacity DC pro daný kmitočtový rozsah se určí ze vzorce

C_max / C_min = f²_max / f²_min

Změnu napětí potřebnou k požadovanému přeladění odečteme z grafu, vzniklého při měření. Musíme ale ještě počítat s kondenzátorem, kterým je laděný obvod oddělen od kapacitní diody, a je zapojen v sérii s potřebnou ladicí kapacitou. Vzorce k výpočtu jsou uvedeny výše.

 

Výhodnou možností je také použít dvojici varikapů, jak je znázorněno na obrázku 6, kde slouží k jemnému dolaďování kmitočtu laděného obvodu oscilátoru L1–C1.

 

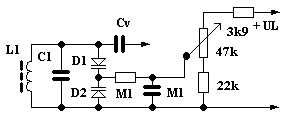
Díky sériovému zapojení obou varikapů je značně zmenšena závislost kmitočtu na amplitudě vf napětí.

 

Výpočet podobných obvodů je opět velmi jednoduchý. Například zde použijeme dva varikapy s kapacitou 20 až 40 pF při změně řídicího napětí od 9V do 2V, změna kapacity je tedy 20 pF. Jestliže rozsah ladění má být kupříkladu 6 %, potřebujeme změnu kapacity 12 %. Z toho si odvodíme celkovou kapacitu laděného obvodu C=20 pF/0,12=167 pF. K této kapacitě si vypočítáme indukčnost cívky dle známého vzorce L=1/(2pf)²*C  (mH, MHz, pF).

Kapacity varikapů jiných typů při různých řídicích napětích je možno zjistit podle přibližného vzorce C=2C₀ / ÖU, kde C₀ = katalogová kapacita uváděná pro napětí 4V, U = použité napětí.

 

Varikapy je také možno s výhodou použít u transceiverů pro obvod t.zv. RIT (Receiver Incremental Tuning), tedy změnu kmitočtu při přechodu z vysílání na příjem, v těchto případech není požadováno velké přeladění. S úspěchem tak můžeme použít zapojení podle následujícího obrázku:

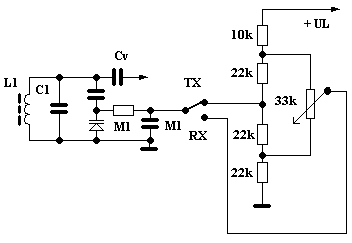
V poloze přepínače TX se na varikap přivádí pevné napětí z děliče. Při přechodu na příjem (v poloze přepínače RX) se napětí přivádí z potenciometru 33k, kterým se dá kmitočet jemně doladit na protistanici. Rozsah přeladění se dá snadno upravit změnou kapacity kondenzátoru zapojeného v sérii s varikapem, nebo změnou hodnot odporů v děliči napětí. Toto zapojení je velmi potřebné zvláště u jednoduchých transceiverů, kdy se po přepnutí na vysílání kmitočet oscilátoru poněkud posune (někdy až o 1 kHz), a když se protistanice, také s transceiverem, na něj doladí, signál uteče zase prvé stanici, takže dojde k efektu perpetua mobile, kdy tyto dvě stanice během jednoho spojení procestují celé pásmo, hihihi....

 

Jednou z dalších možností elektronického ladění, je použití tranzistoru jako spínače. V klasickém zapojení tranzistorového spínače dochází ke skokové změně stavu (tranzistor buď vede, nebo nevede), ovšem zde není použita skoková změna, ale plynulá. Tento trik používal ve svých zařízeních, kde potřeboval větší rozsah ladění, Petr OK1WPN. Možná, že to již bude pozapomenuto, proto jej uvádím pro přehlednost znova. Zapojení pracuje tak, že tranzistor, řízený stejnosměrným napětím z potenciometru postupně otevírá, "zprůchodňuje se", a tím plynule připojuje nebo odpojuje kapacitu C1 v jeho kolektoru. Volbou velikostí C1 a C2 můžeme takto snadno ovlivnit rozsah ladění a to v dosti širokém rozsahu. Navíc je zde velká výhoda v tom, že při použití potenciometru s lineárním průběhem odporu vychází i téměř lineární změna kmitočtu, tedy i průběh stupnice. Kondenzátor zapojený v bázi tranzistoru se volí s kapacitou kolem 10n, slouží pouze k odstranění zbytků vysokofrekvenčního napětí, které se dostanou do obvodu báze. Pracovní odpor v kolektoru se volí v rozsahu 33 – 56 kW.

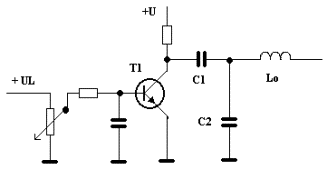
Pokud se použijí kvalitní kondenzátory C1 a C2 (styroflex, nebo raději slída), je i stabilita vyhovující.

 

Navrhování laděných obvodů pro daný kmitočtový rozsah a linearizace průběhu ladění je kapitola sama pro sebe, sice velmi zajímavá, ale vymykající se obsahu tohoto stručného článku. Sledujte tento seriál i dále.