LADĚNÉ  OBVODY 1.

 

V tomto (snad) seriálu článků se mohou začínající "hamateuři" seznámit se základními obvody z vysokofrekvenční radiotechniky. Pokročilejším to asi nic nového nepřinese, těm se předem omlouvám. Vycházím z dlouholetých zkušeností s vedením kroužku radiotechniky na škole, s mladými žáčky.

 

Rozdíl mezi sériovým a paralelním obvodem.

Podívejme se na obrázek 1a a 1b, na nichž jsou schematicky znázorněny paralelní a sériový laděný obvod. Zdá se vám, že je to prakticky totéž, jen poněkud jinak nakreslené? Nojo, je to tak. Jenže takhle vypadají obvody jen v teorii, ve skutečnosti jsou k nim připojeny další

                            

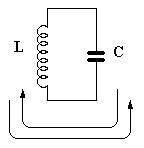
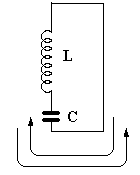
Obrázek 1a                                               Obrázek 1b

 

obvody, jako třeba tranzistor (obrázek 2a, 2b).

                    

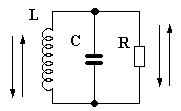
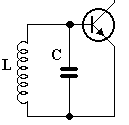
Obrázek 2a                                         Obrázek 2b

 

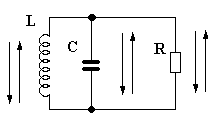
Vnitřek tranzistoru má určitou vodivost, což je převrácená hodnota odporu. Místo tranzistoru si zde tedy představíme odpor. Pro začátek budeme sledovat paralelní laděný obvod na obrázku 3a.

Obrázek 3a

 

V laděném obvodu probíhá tak zvaný cirkulační proud, který se v tomto případě rozvětví (jde samozřejmě cestou menšího odporu) a tedy jeho část protéká i odporem R. Pokud je hodnota odporu R velká, poteče jím jen malý proud a jeho hlavní část bude dále protékat laděným obvodem, na laděném obvodu bude určitá hodnota napětí. Čím je poměr napětí na obvodu větší, tím je větší jakost obvodu – označuje se Q. A podíváme se na druhou verzi: k laděnému obvodu je připojen tranzistor, kterýžto má malý vnitřní odpor. Samozřejmě podle zákona o lenosti přírody poteče větší proud odporem, na laděný obvod jej zbude málo, nakmitá se na něm malé napětí, říkáme že obvod je zatlumen. Činitel jakosti obvodu Q bude žalostně malý.

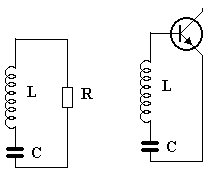
Obrázek 3b

 

No a jak to bude vypadat se sériovým laděným obvodem? Sledujme obrázek 3b, odpor R má vysokou hodnotu. Chudák cirkulační proud, protékající obvodem, má obrovskou práci, aby se odporem protlačil, strašně se unaví a je tedy dosti malý. Dále budeme uvažovat, že odpor R má malou hodnotu. Joj, to se to tomu proudu proudí! Tento obvod má tedy lepší jakost (vyšší Q) než s velkým odporem. A hele, malý vstupní odpor tranzistoru najednou nevadí! Je to dokonce velká výhoda!

 

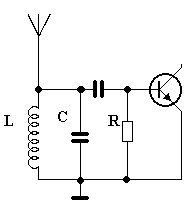
Ještě si ukážeme, jak vypadá v praxi výsledek nízkého či vysokého Q obvodu. Představte si, že máme vstupní laděný obvod přijímače, podle obr. 4. K laděnému obvodu je připojena

Obrázek 4

 

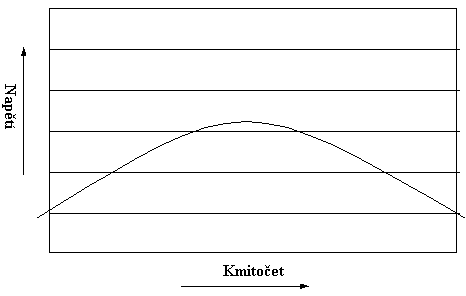
jednak anténa, která také představuje odpor, dále odpor R a vstupní odpor přechodu báze-emitor tranzistoru. Výsledný odpor, připojený k laděnému obvodu je tedy dosti malý a obvod je značně zatlumen. Rezonanční křivka tohoto obvodu pak vypadá jako na obrázku 5, je široká, napětí na obvodu je malé, tím se i na tranzistor dostane malé napětí a přijímaný signál je slabý. Mimo to větší šířka rezonanční křivky způsobí, že kmitočtově blízké signály se nám také dostanou do vstupního tranzistoru přijímače, a pak slyšíme třeba několik stanic najednou.

Úplně jinak to ale vypadá, máme-li vysoké Q laděného obvodu, pak jeho rezonanční křivka vypadá jako na obrázku 6. Vidíme, že se na něm nakmitá větší napětí, křivka je užší, čili kmitočtově blízké stanice mají na vstupu tranzistoru mnohem menší napětí, a již nepřekáží.

Obrázek 5  

 

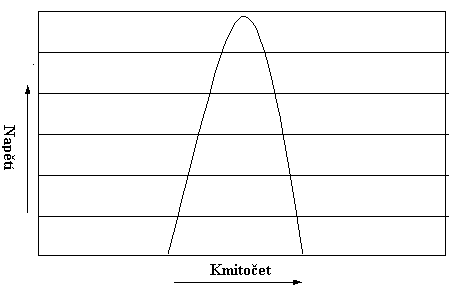
Obrázek 6

 

Tato vlastnost sériových laděných obvodů, že čím menší obvodový odpor tím větší jakost, se využívá především u stabilních oscilátorů, kde je jakost laděného obvodu hlavním požadavkem. Ve vstupních obvodech se spíše používá paralelní laděný obvod, u něhož se provedou vhodná opatření ke snížení vlivu zatěžovacího odporu. Jak? Jistě jste se setkali například s tím, že anténa je k laděnému obvodu navázána buď malou kapacitou, nebo (častěji) pomocí vazební cívky s pár závity. Taktéž vliv vstupního odporu tranzistoru omezíme buď malou vazební kapacitou, připojením báze na odbočku laděného obvodu, nebo na vazební cívku. Připojíme-li tranzistor na odbočku v polovině cívky, pak nám zatěžovací odpor působí jako dvojnásobný (má poloviční vliv), na třetině cívky třetinový vliv, atd. Místo odbočky na cívce je možno použít i kapacitní dělič, podle obrázku 7, který pracuje naprosto stejně jako odbočka.

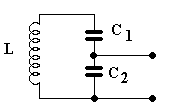
Obrázek 7

 

Parametry laděných obvodů.

Upozorňuji, že toto povídání se týká obou probraných typů laděných obvodů, tedy sériových, i paralelních, prakticky v tom není žádný rozdíl (alespoň z amatérského hlediska).

Kmitočet, na který je laděný obvod naladěn, se určí z tak zvaného Thomsonova vzorce, který je v základním tvaru dosti nepohodlný:

 

f = 1 / ((2 *p) / Ö (L * C))    (Hz, H, F)

 

Jelikož víme (nebo si můžeme jednoduše odvodit) že 1/2*p = 0,1591549431... atd, můžeme si vzorec zjednodušit na

 

f = 159,15 / SQR (L * C)    (MHz, mH, pF) nebo (Hz, H, F)

 

nebo pomocí (1 / 2 * p)²  = 0,02533029591 na častěji používaný tvar

 

f = SQR (25330 / L * C)

 

z čehož si můžeme odvodit, že

C = 25330 / f² *L

L = 25330 / f² * C

 

Co z toho vyplývá? Tak máme například cívku s indukčností 10 mH, a potřebujeme ji naladit na kmitočet dejme tomu 3 MHz. Jednoduše:

 

C = 25330 / 3² * 10 = 284 pF (zaokrouhleno).

 

Nebo ke zjišťování indukčnosti cívek – při rozebírání TV se nám dostala do ruky "nějaká" cívečka, a potřebujeme vědět, jakou má indukčnost, jestli se hodí tak jak je, nebo ji bude nutno převinout. K cívce připojíme paralelně nějaký kondenzátor se známou kapacitou. Použijeme Dip Oscilátor (ssací měřič rezonance) ke zjištění rezonančního kmitočtu, zjistíme třeba, že s kondenzátorem 100 pF rezonuje na 5 MHz. A jedeme na to:

 

L = 25330 / 5² * 100 = 10 mH

Jednoduché jak facka, žejo?

Není? A sakra, vy nemáte Dip Oscilátor!!! Ale to je tedy velká chyba. To je totiž základní přístroj, bez něhož se při práci s vf obvody téměř neobejdete. Měli by jste si jej pořídit hned po univerzálním měřicím přístroji U – I – R (multimetr, doporučuji ručičkový). Nojo, takže některý příští článeček z této série bude věnován jeho stavbě, můžete se těšit.

Pro ty z vás, kteří předešlé povídání již vstřebali a chtěli by něco konkrétního, uvádím pár stručných vzorečků, jak na to.

 

Vazba s anténou na odbočku cívky.

K neladěné anténě (v amatérských podmínkách velice častý případ, obvyklá hodnota impedance antény bývá kolem 200 ohmů) volíme:

 

% závitů odbočky = 0,25 * SQR (C * f)

 

kde SQR značí odmocninu, C je kapacita laděného obvodu (v pF) a f střední pracovní kmitočet (MHz).

 

Příklad: f = 7MHz, C=120 pF, cívka má 20 závitů.

              % odbočky = 0,25 * odmocnina z (120 * 7) = 7,3 %.

              Závitů odbočky = 20 / 100 * 7,3 = 1,5

              Odbočka pro připojení antény je na 1,5 závitu vstupní cívky od uzemněného konce.

 

Vazba s anténou pomocí vazební cívky.

L_vaz = Z_o / (w * Q_o * k²)   (mH, W, MHz)

kde k je koeficient vazby obou cívek. Pokud jsou vinuty na sobě, je tedy těsná vazba, pak k=0,4 až 0,5. Pro volnou vazbu, kdy jsou cívky na stejné kostře vedle sebe ale s mezerou mezi oběma vinutími, je k < 0,1. V běžných případech se volí k = 0,2 až 0,3, cívky jsou vinuty vedle sebe.

 

Vazba pomocí kapacitního děliče.

Je to v podstatě také transformace impedancí, často používaná ve vysílací technice k vzájemné vazbě jednotlivých stupňů, nebo pro výstup signálového napětí z oscilátoru (viz obrázek 7).

p = C₂ / C₁

C = 1 / (1 / C₁ + 1 / C₂)

Z toho tedy:

C₁ = C / p *(1 + p)

C₂ = C₁ * p

kde C je celková ladicí kapacita obvodu.

 

Příště se budeme věnovat blíže praktickým otázkám laděných obvodů, volbám jednotlivých součástí a úpravám jejich hodnot, rozprostřenému ladění a podobně.