DĚLIČ NAPĚTÍ
Děliče napětí umožňují rozdělit větší napětí na menší (třeba i několik), a to jak u stejnosměrného, tak i u střídavého napětí.

Obrázek 1:Princip jednoduchého děliče napětí.
Nejjednodušší dělič napětí dodává na výstupu nejméně dvě napětí. Pokud jsou hodnoty odporů stejné, tak podle Ohmova zákona napětí na jeho výstupu bude poloviční oproti vstupnímu, čili úbytek napětí na obou odporech bude stejný.
V ostatních případech hodnota úbytku napětí na jednotlivých odporech děliče vyplývá ze vzorce:
UR1 = I*R1; UR2 = I*R2 (1)
Kde UR1, UR2 - hodnota úbytku napětí na odporech R1 a R2, I je proud v obvodu.
V zapojení děličů se výstupní napětí obvykle snímá z dolního (podle schématu) odporu proti společnému vodiči. Součet úbytků napětí UR1, UR2na odporech se rovná napájecímu napětí UZ. Proud v obvodu děliče se rovná napájecímu napětí děleno součtem odporů R1 a R2.
I = UZ / (R1 + R2) (2)
Ukažme si praktické provedení děliče napětí (obrázek 2):
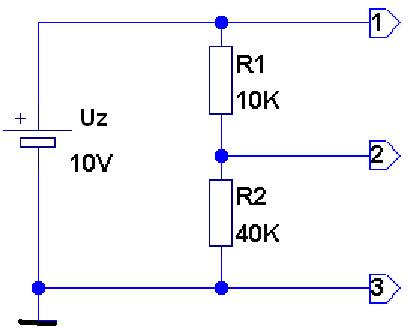
Obrázek 2: Dělič stejnosměrného napětí.
Proud protékající obvodem v tomto zapojení podle vzorce (2) bude roven
I = 10 / (10 000+40 000) = 0,0002 А = 0,2 mА.
Takže dle vzorce (1) bude úbytek napětí na odporech tohoto děliče roven:
UR1
= 0,0002*10 000 = 2 V;
UR2 = 0,0002*40 000 = 8 V.
Pokud ze vzorce (1) odvodíme proud:
I = UR1 / R1 (3)
A doplníme hodnoty do vzorce (2), získáme univerzální vzorec pro výpočet napěťového děliče:
UR1 / R1 = UZ / (R1 + R2)
Odkud
UR1 = UZ * R1 / (R1 + R2) (4)
Dosazením hodnot napětí a odporů ve vzorce (4), získáme hodnotu napětí na odporu R1:
UR1 = 10 * 10 000 / (10 000 + 40 000) = 2 V,
A na odporu R2:
UR2 = 10 * 40 000 / (10 000 + 40 000) = 8 V.
Dělič napětí s prvky s rozprostřenými parametry v obvodu střídavého proudu.
Ve výše uvedeném schématu byly použity pro dělič napětí odporové prvky (odpory, rezistory), tedy prvky se soustředěnými parametry, viz obrázek 2, s napájením stejnosměrným napětím (i když tento obvod může být napájen i střídavým napětím). Stejně tak ale můžeme v děliči použít prvky s rozprostřenými parametry (kondenzátory, cívky) ale v tom případě musí být obvod napájen pouze střídavým sinusovým napětím (obrázek 3).
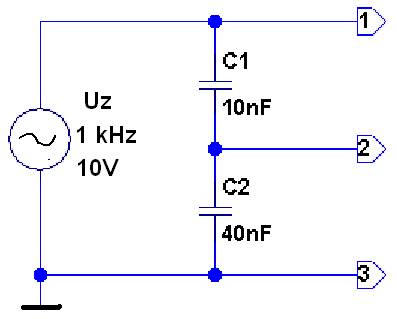
Obrázek 3 – Kapacitní dělič napětí v obvodu střídavého napětí
Kapacitní dělič z obrázku 3 pracuje podobně, jako dříve uvedený odporový dělič, ale vypočítává se trochu jinak, jelikož reaktance kondenzátoru je nepřímo úměrná jeho kapacitě:
Rc = 1/(2 * π * f * C)
Kde Rc je reaktance (zdánlivý odpor) kondenzátoru,
π – Ludolfovo číslo = 3,14159……
f – kmitočet napětí se sinusovým průběhem v Hertzích (H).
C – kapacita kondenzátoru ve Faradech (F).
Z čehož vyplývá, že čím je větší kapacita kondenzátoru, tím menší odpor klade střídavému proudu, a tudíž dělič napětí obvodu s kondenzátory s velkou kapacitou bude úbytek napětí menší, než na kondenzátoru s malou kapacitou. Proto vzorec (4) pro kapacitní dělič napětí bude mít následující tvar:
UС1 = Un * С2 / (С1 + С2) (5)
čili
UС1
= 10 * 40*10-9 / (10*10-9+40*10-9) = 8 V,
UС2 = 10 * 10*10-9 / (10*10-9+40*10-9)
= 2 V.
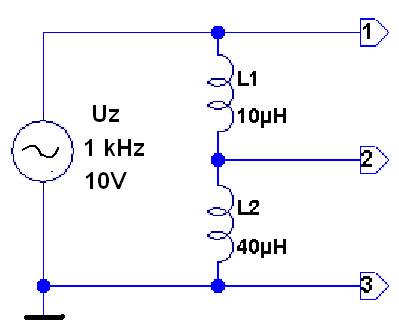
Obrázek 4 – Induktivní dělič napětí v obvodu střídavého napětí
Reaktance cívky v obvodu střídavého proudu v poměru k jmenovité indukčnosti je:
RL = 2 * π * f * L
Kde RL - reaktance cívky;
π (Ludolfovo číslo pi) = 3,14159
...;
f - kmitočet sinusového napětí, Hz;
L - indukčnost cívky, Henry.
Z předchozího vyplývá, že vzorec pro výpočet indukčního děliče napětí bude
přesně stejný jako vzorec pro výpočet děliče odporová napětí (4), kde bude
použita hodnota indukčnosti namísto hodnoty odporu:
UL1 = Uz * L1 / (L1 + L2)
(6)
Po dosazení parametrů prvků z obrázku 4 do vzorce (6) dostaneme:
UL1
= 10 * 10 * 10-6 / (10 * 10-6 + 40 * 10-6) = 2 V,
UL2 = 10 * 40 * 10-6 / (10 * 10-6 + 40 * 10-6) = 8 V.
Na závěr je třeba poznamenat, že ve všech výpočtech byla velikost zátěže uvažována jako nekonečná, takže vypočtené hodnoty platí pouze tehdy, je-li uvažovaná podskupina odporů zátěže mnohokrát větší než je hodnota jejich vlastních odporů.