Co to je decibel (dB)
Decibel (dB). Velmi často se zaměňuje se zvukem. Mnohými je považován za nepřítele a zbytečnou komplikaci. Je to záhadné a tajemné zaklínadlo, které dosti lidí rádo používá, aniž by však vědělo o čem je vlastně řeč. Uvědomte si, že pojem decibelu je pro ty, kteří jej pochopí, všeobecně použitelný v mnoha oblastech vědy a techniky.
Původní označení Bel (B) je pro praktické účely poněkud velké, takže byla všeobecně přijata jeho desetina, ale upozorňuji, že to rozhodně není žádná jednotka, pouze vyjádření poměru dvou hodnot. Mohlo by to být třeba i poměr výšky jednoho stromu k výšce druhého. Samozřejmě, že se tyto výrazy dají použít i v elektronice (a radiotechnice), stejně, jako téměř ve všech ostatních oborech. Podmínkou je, že onen poměr musí být označen pouze dvěma písmeny, jako „dB“. Každý další znak jen upřesňuje o co se jedná, o poměr čeho. Matematicky to je:
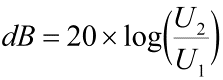nebo obráceně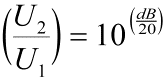 
neboli pro případ poměru výkonů:
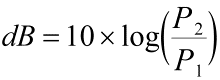nebo obráceně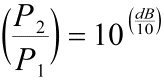 
Číslo 10 je v prvém případě nahrazeno číslem 20, vzhledem k tomu, že zde se jedná o poměr výkonů, jak je zřejmé z jednoduchých počtů. V případě, že napětí při konstantním zatížení zvýší 10, ve stejném poměru se zvýší také proud. Vzhledem k tomu, že výkon je složen jak z napětí, tak i z proudu, tedy se zvýší 10 x 10 = 100 . 20dB tedy znamená desetinásobné vzrůst napětí, což způsobí 100-násobné zvýšení napětí, a tím i rozdíl. To je důležité nejen pro přepočet lineárních vztahů "dB" a naopak, ale i vzrůst napětí, řekněme o 12 dB má za následek stejný (12 dB) nárůst výkonu při konstantní impedancí.
Proč si komplikovat život jeho používáním?
Ve skutečnosti, to je docela významné zjednodušení mnoha výpočtů souvisejících s elektronikou, rádiem, atd. Totiž zdlouhavé výpočty jako zisk (a útlum) kaskádově zapojených obvodů (zesilovače, filtry, útlumové články atd.) prováděné pomocí násobení a dělení velkých hodnot, jsou nahrazeny relativně jednoduchým sečítáním a odečítáním čísel. Ony totiž úrovně signálů v elektronice a radiotechnice jsou tak rozdílné, že v praxi poměr mezi nejmenším a největším výkonem dosahuje 1 : 100 000 000. A teď pracujte a počítejte s takovými čísly, když samozřejmě jednodušeji to jde s decibely. Ve většině případů mohou být tyto výpočty prováděny z paměti, a když není nutná vysoká přesnost, ani pro převod z tradiční lineární velikosti na decibely nepotřebují kalkulačku. Je to samozřejmě jednoduché, když si zapamatujeme několik základních podmínek. Tak například, že poměr výkonů 1 : 2 je 3 dB, nebo že například že poměr výkonů 1 : 10 je 10 dB, atd.
Několik příkladů výsledků (například zisk v obvodu):
10 krát = 20dB (10dB výkon)
100 krát = 40dB (20dB výkon)
1000 krát = 60dB (30dB výkon)
1000000 krát = 120dB (60dB výkon), atd.
Zde je vidět, že každá nula má hodnotu 20 dB (10 dB na výkonu).
Příklady poměrů dvou záporných hodnot, například ztráty v obvodu:
1/10 (0,1) krát = – 20dB (– 10dB výkon)
1/100 (0,01) krát = – 40dB (– 20dB výkon)
1/1000 (0,001) krát = – 60dB (– 30dB výkon), atd.
Opět platí, že každá nula má hodnotu 20 dB (10 dB výkonově) odečtenou (ne děleno).
Samozřejmě, že použití vztahu pouze pro násobky 20 dB (10 db pro výkon) není příliš přesné, ale může to být lepší. Několik příkladů (hodnoty jsou zaokrouhlené):
1.41 krát = 3dB (1.5dB výkon)
2 krát = 6dB (3dB výkon)
3.16 krát = 10dB (5dB výkon) (používá se přibližně 3 krát).
Jak je to možno použít v praxi?
Postačí si zapamatovat několik takových příkladů s převody na dB a zpět.
4 krát = 2 × 2 = 6dB + 6dB = 12dB
5 krát = 10 / 2 = 20dB – 6dB = 14dB
8 krát = 2 × 2 × 2 = 6dB + 6dB + 6dB = 18dB
25 krát = 5 × 5 = 14dB + 14dB = 28dB
30 krát = 10 × 3 = 20dB + 10dB = 30dB
200 krát = 100 × 2 = 40dB + 6dB = 46dB
A několik příkladů konverze dB na lineární vztah (ne výkony):
26dB = 20dB + 6dB = 10 × 2 = 20 krát
54dB = 60dB – 6dB = 1000 / 2 = 500 krát
22dB = 10dB + 6dB + 6dB = 3 × 2 × 2 = 12 krát
30dB = 20dB + 10dB = 10 × 3 = 30 krát
– 36dB = – 30dB – 6dB – 1 / (30 × 2) = 1 / 60 krát
Jsou to samozřejmě hodnoty přibližné, získané bez kalkulačky, ale v mnoha případech (řekl bych že téměř ve všech) nějak extrémně vysoká přesnost není zapotřebí. Stejně tak můžeme samozřejmě pracovat i s výkonovými vztahy.
0dBm = 1 mW
Velmi často se výraz „dB“ používá s dalšími dodatkovými písmeny, nebo s čísly. V těchto případech se vyjadřuje poměr hodnot v nějakém jiném formátu nazvaném doplňkovými písmeny.
Příklady:
30 dBm = 1 000 mW = 1 W
- 30 dBm = 1/1 000 mW = 1 uW
Toto je velmi často používáno v oboru měření vysokých kmitočtů. Požadujete-li převod na napětí, je zapotřebí znát odpor (tedy impedanci) zátěže. Pokud se například rovná (ve většině případů vf techniky) 50 Ohmů, jednoduchý výpočet ukáže, že to je kolem 224 mV.
0dBW = 1W
Jednotka výkonu vysokých kmitočtů je často používána k definování limitu normálního výkonu (je to výkon, proto se násobí 10 a ne 20).
Příklady:
60dBW = 1MW (1 Megawatt)
–30dBW = 1 / 1 000W = 1mW (čili –30dBW = 0dBm)
0dBV = 1V
Jednotka často používaná pro měření akustických zařízení. Ve skutečnosti není možné přímo nahradit jednotku výkonu (je to vlastně jednotka napětí), ale velmi často se používá v systémech s impedancí 600 Ohmů (ale nejenom).
Příklady:
6dBV = 2V
– 60dBV = 1 / 1000V = 1mV
0dBµV = 1µV
Tato jednotka se často používá pro měření vysokofrekvenčního napětí, typicky při měření rádiových zařízení, antén a podobně. Zpravidla se používá v systémech s impedancí 50 ohmů, takže, takže může být přímo převedena na jednotky výkonu, například 0 dBm = 107 dBμV (samozřejmě pouze v systémech 50 ohmů). Odkud se vzalo ono záhadné číslo 107 je vysvětleno v poznámkách na konci článku.
Příklad:
120dBµV = 1000000µV = 1V = 1dBV
V mnoha případech je možno přidat další písmeno (písmena) k základu dB, což pak vyjadřuje poměr velikosti naměřené hodnoty.
Pro zajímavost zisky některých antén udané proti půlvlnému dipólu.
anténa 1/4 = -1,8 dBd
anténa 1/2 = 0,0 dBd
anténa 5/8 = + 1,2 dBd
anténa 7/8 = + 2,4 dBd
Udaje jsou platné pro antény správně nastavené a v ideálním prostředí.
VE3ABX